2018-2019学年数学北师大版八年级上册4.1《函数》 同步练习
试卷更新日期:2018-09-30 类型:同步测试
一、选择题
-
1. 在圆的周长C=2πR中,常量与变量分别是( )A、2是常量,C、π、R是变量 B、2π是常量,C、R是变量 C、C、2是常量,R是变量 D、2是常量,C、R是变量2. 在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )A、太阳光强弱 B、水的温度 C、所晒时间 D、热水器3. 甲、乙两地相距s千米,某人行完全程所用的时间t(时)与他的速度v(千米/时)满足vt=s,在这个变化过程中,下列判断中,错误的是( )A、s是变量 B、t是变量 C、v是变量 D、s是常量4. 已知两个变量x和y,它们之间的3组对应值如下表所示
x
﹣1
0
1
y
﹣1
1
3
则y与x之间的函数关系式可能是( )
A、y=x B、y=2x+1 C、y=x2+x+1 D、5. 汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速路,继续以100千米/时的速度匀速行驶,则汽车行驶的路程s(千米)与行驶的时间t(时)的函数关系的大致图象是( )A、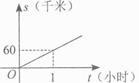 B、
B、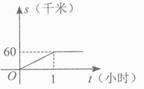 C、
C、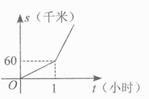 D、
D、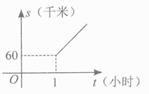
二、填空题:
-
6. 等腰三角形的顶角y与底角x之间是函数关系吗?(选是或不是)7. 火车以40千米/时的速度行驶,它走过的路程s(千米)与时间t(小时)之间的关系式 ,其中自变量是 , 因变量是 .
8. 对于圆的周长公式c=2πr,其中自变量是 , 因变量是 .9. 写出下列变化过程中的函数关系式,指出式子中的自变量及自变量的取值范围.(1)、某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元,求出租车车费y(元)与行程x(千米)之间的函数关系式;(不足1千米按1千米计)
(2)、等腰三角形顶角y与底角x之间的关系10. 放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.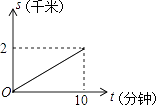
三、解答题
-
11. 一辆汽车油箱内有油48升,从某地出发,每行1km,耗油0.6升,如果设剩油量为y(升),行驶路程为x(千米).
(1)、写出y与x的关系式;
(2)、这辆汽车行驶35km时,剩油多少升?汽车剩油12升时,行驶了多千米?
12. 在国内投寄平信应付邮资如下表: (1)、y是x的函数吗?为什么?
(1)、y是x的函数吗?为什么?
(2)、分别求当x=5,10,30,50时的函数值.
13. 地壳的厚度约为8到40km,在地表以下不太深的地方,温度可按y=3.5x+t计算,其中x是深度,t是地球表面温度,y是所达深度的温度.
(1)、在这个变化过程中,自变量和因变量分别是什么?(2)、如果地表温度为2℃,计算当x为5km时地壳的温度.14. 张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿,返回途中在读报栏前看了一会儿报,如图是据此情境画出的图象,请你回答下面的问题: (1)、张爷爷是在什么地方碰到老邻居的,交谈了多长时间?(2)、读报栏大约离家多远?(3)、图中反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?15. 弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
(1)、张爷爷是在什么地方碰到老邻居的,交谈了多长时间?(2)、读报栏大约离家多远?(3)、图中反映了哪些变量之间的关系?其中哪个是自变量?哪个是因变量?15. 弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:物体的质量(kg)
0
1
2
3
4
5
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
(1)、上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?(2)、当物体的质量为3kg时,弹簧的长度怎样变化?(3)、当物体的质量逐渐增加时,弹簧的长度怎样变化?(4)、如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)、当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.