备考2019年高考数学一轮专题:第7讲 二次函数与幂函数
试卷更新日期:2018-09-27 类型:一轮复习
一、单选题
-
1. 在同一直角坐标系中,函数y=mx+m和函数y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、
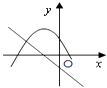 B、
B、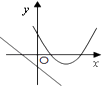 C、
C、 D、
D、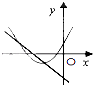 2. 在同一坐标系内,函数 和 的图象可能是( )A、
2. 在同一坐标系内,函数 和 的图象可能是( )A、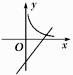 B、
B、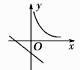 C、
C、 D、
D、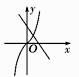 3. 函数y=2x2﹣6x+3,x∈[﹣1,1],则y的最小值是( )A、﹣ B、3 C、﹣1 D、不存在4. 已知函数f(x)=(m2-m-5)xm是幂函数,且在x∈(0,+∞)上为增函数,则实数m的值是( )A、-2 B、4 C、3 D、-2或35. 已知反比例函数y= 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致为( )
3. 函数y=2x2﹣6x+3,x∈[﹣1,1],则y的最小值是( )A、﹣ B、3 C、﹣1 D、不存在4. 已知函数f(x)=(m2-m-5)xm是幂函数,且在x∈(0,+∞)上为增函数,则实数m的值是( )A、-2 B、4 C、3 D、-2或35. 已知反比例函数y= 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致为( ) A、
A、 B、
B、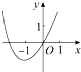 C、
C、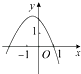 D、
D、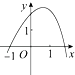 6. 二次函数f(x)=ax2+bx+c的图象开口向下,对称轴为x=1,图象与x轴的两个交点中,一个交点的横坐标x1∈(2,3),则有
6. 二次函数f(x)=ax2+bx+c的图象开口向下,对称轴为x=1,图象与x轴的两个交点中,一个交点的横坐标x1∈(2,3),则有( )
A、abc>0 B、a+b+c<0 C、a+c<b D、3b<2c7. 已知点 在幂函数 的图象上,设 ,则 的大小关系为( )A、 B、 C、 D、8. 已知函数y=ax2+bx+c,如果c>b>a,且a+b+c=0,则它的图象是( )A、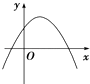 B、
B、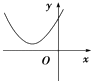 C、
C、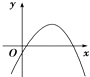 D、
D、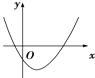 9. 函数y=x2﹣4x+3,x∈[0,3]的值域为( )A、[0,3] B、[﹣1,0] C、[﹣1,3] D、[0,2]10. 设抛物线y=x2+ax﹣2的对称轴方程为x=1,则该抛物线顶点坐标为( )A、(1,﹣3) B、(1,﹣1) C、(1,0) D、(﹣1,﹣3)11. 已知幂函数 的图像经过点 ,则 的值等于( )
9. 函数y=x2﹣4x+3,x∈[0,3]的值域为( )A、[0,3] B、[﹣1,0] C、[﹣1,3] D、[0,2]10. 设抛物线y=x2+ax﹣2的对称轴方程为x=1,则该抛物线顶点坐标为( )A、(1,﹣3) B、(1,﹣1) C、(1,0) D、(﹣1,﹣3)11. 已知幂函数 的图像经过点 ,则 的值等于( )
A、 B、 C、 D、12. 已知m>2,点(m﹣1,y1),(m.y2),(m+1,y3)都在二次函数y=x2﹣2x的图象上,则( )A、y1<y2<y3 B、y3<y2<y1 C、y1<y3<y2 D、y2<y1<y3二、填空题
-
13. 已知函数f(x)=3xa﹣2﹣2的图象过点(2,4),则a= .14. 如果幂函数 的图象不过原点,则m的值是15. 已知函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,3)和(1,1)两点,若0<c<1,则a的取值范围是 .16. 若y=xn的图象在x>1时,位于y=x的上方,则n的取值范围是 .
三、解答题
-
17. 如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是 .
 (1)、用宽 (单位 )表示所建造的每间熊猫居室的面积 (单位 );(2)、怎么设计才能使所建造的每间熊猫居室面积最大?并求出每间熊猫居室的最大面积?18. 已知函数f(x)=x2+(2a﹣1)x﹣3.(1)、当a=2,x∈[﹣2,3]时,求函数f(x)的值域.(2)、若函数f(x)在[﹣1,3]上单调递增,求实数a的范围.
(1)、用宽 (单位 )表示所建造的每间熊猫居室的面积 (单位 );(2)、怎么设计才能使所建造的每间熊猫居室面积最大?并求出每间熊猫居室的最大面积?18. 已知函数f(x)=x2+(2a﹣1)x﹣3.(1)、当a=2,x∈[﹣2,3]时,求函数f(x)的值域.(2)、若函数f(x)在[﹣1,3]上单调递增,求实数a的范围.