河北省张家口市2017-2018学年高二下学期文数期末考试试卷
试卷更新日期:2018-09-27 类型:期末考试
一、单选题
-
1. 已知全集 , , ,则 ( )
A、 B、 C、 D、2. 已知复数 ( 是虚数单位),则 ( 是 的共轭复数)的虚部为( )A、 B、 C、 D、3. 已知命题 : ,使得 ,则 为( )A、 ,总有 B、 ,使得 C、 ,总有 D、 ,使得4. 下面四个推导过程,符合演绎推理三段论形式且推理正确的是( )A、大前提:分数是有理数;小前提: 是有理数;结论: 是分数 B、大前提:分数是有理数;小前提: 是分数;结论: 是有理数 C、大前提: 是分数;小前提:分数是有理数;结论: 是有理数 D、大前提: 是分数;小前提: 是有理数;结论:分数是有理数5. 执行如图所示的程序框图,如果输出结果为 ,在空白判断框中的条件是( ) A、 B、 C、 D、6. 若 , , ,则( )A、 B、 C、 D、7. 已知命题 : ,命题 : ,且 是 的必要不充分条件,则实数 的取值范围是( )A、 B、 C、 D、8. 将函数 的图象向左平移1个单位得到曲线 ,而且曲线 与函数 的图象关于 轴对称,则 的表达式为( )A、 B、 C、 D、9. 下面推理过程中使用了类比推理方法,其中推理正确的是( )A、平面内的三条直线 ,若 ,则 .类比推出:空间中的三条直线 ,若 ,则 B、平面内的三条直线 ,若 ,则 .类比推出:空间中的三条向量 ,若 ,则 C、在平面内,若两个正三角形的边长的比为 ,则它们的面积比为 .类比推出:在空间中,若两个正四面体的棱长的比为 ,则它们的体积比为 D、若 ,则复数 .类比推理:“若 ,则 ”10. 定义在 上的奇函数 满足 ,并且当 时, ,则 ( )
A、 B、 C、 D、6. 若 , , ,则( )A、 B、 C、 D、7. 已知命题 : ,命题 : ,且 是 的必要不充分条件,则实数 的取值范围是( )A、 B、 C、 D、8. 将函数 的图象向左平移1个单位得到曲线 ,而且曲线 与函数 的图象关于 轴对称,则 的表达式为( )A、 B、 C、 D、9. 下面推理过程中使用了类比推理方法,其中推理正确的是( )A、平面内的三条直线 ,若 ,则 .类比推出:空间中的三条直线 ,若 ,则 B、平面内的三条直线 ,若 ,则 .类比推出:空间中的三条向量 ,若 ,则 C、在平面内,若两个正三角形的边长的比为 ,则它们的面积比为 .类比推出:在空间中,若两个正四面体的棱长的比为 ,则它们的体积比为 D、若 ,则复数 .类比推理:“若 ,则 ”10. 定义在 上的奇函数 满足 ,并且当 时, ,则 ( )
A、 B、 C、 D、11. 且 , 可进行如下“分解”:若 的“分解”中有一个数是2019,则 ( )
A、44 B、45 C、46 D、4712. 函数 ,若函数 三个不同的零点,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 设 ,则 .14. 已知函数 的定义域和值域都为 ,则 .15. 执行如图程序框图,输出的结果为.
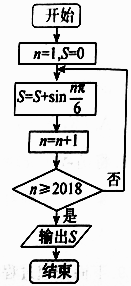 16. 函数 ,其中 ,若对任意正数 都有 ,则实数 的取值范围为.
16. 函数 ,其中 ,若对任意正数 都有 ,则实数 的取值范围为.三、解答题
-
17. 已知复数 , 是 的共轭复数,且 为纯虚数, 在复平面内所对应的点 在第二象限,求 .18. 已知 ,求证:(1)、 ;(2)、 .19. 函数 及其图象上一点 .
(1)、若直线 与函数 的图象相切于 ,求直线 的方程;(2)、若函数 的图象的切线 经过点 ,但 不是切点,求直线 的方程.
20. 已知 ,函数 ( 是自然对数的底数).(1)、若 有最小值,求 的取值范围,并求出 的最小值;(2)、若对任意实数 ,不等式 恒成立,求实数 的取值范围.21. 在平面直角坐标系 中,曲线 的参数方程为 ( 为参数),曲线 的参数方程为 ( 为参数),以坐标原点 为极点, 轴正半轴为极轴建立极坐标系,直线 的极坐标方程为 ,直线 与曲线 交于 两点,直线 与曲线 交于 两点.(1)、当 时,求 两点的极坐标;(2)、设 ,求 的值.