河北省邯郸市2017-2018学年高二下学期文数期末考试试卷
试卷更新日期:2018-09-27 类型:期末考试
一、单选题
-
1. 已知 , ,则 ( )A、 B、 C、 D、2. ( )A、 B、 C、 D、3. 设 ,则 =( )A、 B、 C、 D、4. “ ”是“ ”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件5. 已知 ,则 ( )A、 B、 C、 D、6. 设 的内角 , , 所对的边分别为 , , ,若 ,则 的形状为( )A、锐角三角形 B、直角三角形 C、等边三角形 D、等腰三角形7. 函数 满足 ,且当 时, ,则 的值为( )A、 B、 C、 D、8. 若函数 在区间 单调递增,则 的取值范围是( )
A、 B、 C、 D、9. 函数 的部分图象如图所示,则( ) A、 B、 C、 D、10. 若函数 ( )图象的一个对称中心是 ,则 的最小值为( )A、1 B、2 C、4 D、811. 函数 的图象的大致形状是( )A、
A、 B、 C、 D、10. 若函数 ( )图象的一个对称中心是 ,则 的最小值为( )A、1 B、2 C、4 D、811. 函数 的图象的大致形状是( )A、 B、
B、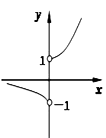 C、
C、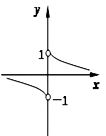 D、
D、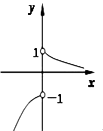 12. 已知函数 ( , , )的图像与 轴交于点 ,在 轴右边到 轴最近的最高坐标为 ,则不等式 的解集是( )
12. 已知函数 ( , , )的图像与 轴交于点 ,在 轴右边到 轴最近的最高坐标为 ,则不等式 的解集是( )
A、 , B、 , C、 , D、 ,二、填空题
-
13. 已知命题 : ,总有 .则 为 .14. 不等式 的解集是 .15. 曲线 在点 处的切线方程为 .16. 若动直线 与函数 和 的图象分别交于 , 两点,则 的最大值为 .
三、解答题
-
17. 在 中, , , 的对边分别为 , , ,若 ,(1)、求 的大小;(2)、若 , ,求 , 的值.18. 已知向量 , , ,设函数 .(1)、求 的最小正周期;(2)、求函数 的单调递减区间;(3)、求 在 上的最大值和最小值.19. 某贫困地区有1500户居民,其中平原地区1050户,山区450户,为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元)
(I)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为 , , , , , .如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
附:
0.100
0.050
0.010
0.001
2.706
3.841
6.635
10.828
超过2万元
不超过2万元
总计
平原地区
山区
5
总计
 20. 如图,某军舰艇位于岛的 的正西方 处,且与岛的 相距12海里.经过侦察发现,国际海盗船以10海里/小时的速度从岛屿 出发沿北偏东30°方向逃窜,同时,该军舰艇从 处出发沿北偏东 的方向匀速追赶国际海盗船,恰好用2小时追上.
20. 如图,某军舰艇位于岛的 的正西方 处,且与岛的 相距12海里.经过侦察发现,国际海盗船以10海里/小时的速度从岛屿 出发沿北偏东30°方向逃窜,同时,该军舰艇从 处出发沿北偏东 的方向匀速追赶国际海盗船,恰好用2小时追上.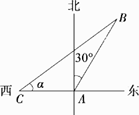 (1)、求该军舰艇的速度.(2)、求 的值.
(1)、求该军舰艇的速度.(2)、求 的值.