河北省邯郸市2017-2018学年高二下学期理数期末考试试卷

试卷更新日期：2018-09-27 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {(x ， y) | x^{2} + y^{2} = 1}$ ， $B = {(x ， y) | y = x}$ ，则 $A \cap^{} B$ 中元素的个数为（）

A、3 B、2 C、1 D、0

查看试题解析
2. 设复数 $z_{1}$ ， $z_{2}$ 在复平面内的对应点关于虚轴对称， $z_{1} = 2 + i$ ，则 $z_{1} z_{2} =$ （）

A、 $- 4 + i$ B、5 C、-5 D、 $- 4 - i$

查看试题解析
3. “ $ln x > ln y$ ”是“ $x > y$ ”的（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看试题解析
4. 正数 $a 、 b 、 c$ 满足 ${log}_{2} a = {log}_{3} b = - {log}_{5} c > 0$ ，则（）

A、 $a < b < c$ B、 $a < c < b$ C、 $c < a < b$ D、 $c < b < a$

查看试题解析
5. 命题“ $\forall n \in N^{*} ， f (n) \in N^{*}$ 且 $f (n) \leq n$ 的否定形式是（）

A、 $\forall n \in N^{*} ， f (n) \in N^{*}$ 且 $f (n) > n$ B、 $\forall n \in N^{*} ， f (n) \in N^{*}$ 或 $f (n) > n$ C、 $\exists n_{0} \in N^{*} ， f (n_{0}) \in N^{*}$ 且 $f (n_{0}) > n_{0}$ D、 $\exists n_{0} \in N^{*} ， f (n_{0}) \in N^{*}$ 或 $f (n_{0}) > n_{0}$

查看试题解析
6. 设 $Δ A B C$ 的内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，若 $b cos C + c cos B = a sin A$ ，则 $Δ A B C$ 的形状为（）

A、锐角三角形 B、直角三角形 C、等边三角形 D、等腰三角形

查看试题解析
7. 已知函数 $f (x) = sinA (ω x + φ) + b$ （ $A > 0$ ， $ω > 0$ ）的图象如图所示，则 $f (x)$ 的解析式为（）

A、 $f (x) = 2 sin (\frac{π}{6} x + \frac{π}{3}) + 2$ B、 $f (x) = 3 sin (\frac{1}{3} x - \frac{π}{6}) + 2$ C、 $f (x) = 2 sin (\frac{π}{6} x + \frac{π}{6}) + 3$ D、 $f (x) = 2 sin (\frac{π}{6} x + \frac{π}{3}) + 3$

查看试题解析
8. 设函数 $f (x)$ ， $g (x)$ 的定义域都为R，且 $f (x)$ 是奇函数， $g (x)$ 是偶函数，则下列结论中正确的是（）

A、 $f (x) g (x)$ 是偶函数 B、| $f (x)$ | $g (x)$ 是奇函数 C、 $f (x)$ | $g (x)$ |是奇函数 D、| $f (x) g (x)$ |是奇函数

查看试题解析
9. 设函数 $f (x) = {\begin{matrix} 1 + {log}_{2} (2 - x) ， x < 1 ， \\ 2^{x - 1} ， x \geq 1 ， \end{matrix}$ ， $f (- 2) + f ({log}_{2} 12) =$ （）

A、3 B、6 C、9 D、12

查看试题解析
10. 已知函数 $f (x) = cos (x + φ)$ $(0 < | φ | < \frac{π}{2})$ ， $f (x + \frac{π}{4})$ 是奇函数，则（）

A、 $f (x)$ 在 $(\frac{π}{4} ， π)$ 上单调递减 B、 $f (x)$ 在 $(0 ， \frac{π}{4})$ 上单调递减 C、 $f (x)$ 在 $(\frac{π}{4} ， π)$ 上单调递增 D、 $f (x)$ 在 $(0 ， \frac{π}{4})$ 上单调递增

查看试题解析
11. 函数 $f (x) = \frac{ln (x^{2} - 4 x + 4)}{{(x - 2)}^{3}}$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
12. 直线 $y = a$ 分别与直线 $y = 2 x + 2$ ，曲线 $y = x + ln x$ 交于点 $A 、 B$ ，则 $| A B |$ 的最小值为（）

A、3 B、2 C、 $\frac{3 \sqrt{2}}{4}$ D、 $\frac{3}{2}$

查看试题解析

二、填空题

13. 已知向量 $\overset{⇀}{a} = (1 ， 2)$ ， $\overset{⇀}{b} = (x ， - 1)$ ，若 $\overset{⇀}{a} ∥ (\overset{⇀}{a} - \overset{⇀}{b})$ ，则 $\overset{⇀}{a} \cdot \overset{⇀}{b} =$ ．

查看试题解析
14. 不等式 ${(\frac{1}{2})}^{x^{2} - 3} < 2^{- 2 x}$ 的解集是．

查看试题解析
15. 已知 $sin α + cos β = 1$ ， $cos α + sin β = 0$ ，则 $sin (α + β)$ ．

查看试题解析
16. 三角形 $A B C$ 中， $D$ 是 $B C$ 边上一点， $∠ B A D = ∠ D A C = 60 °$ ， $B C = 7$ ，且三角形 $A B D$ 与三角形 $A D C$ 面积之比为 $\frac{5}{3}$ ，则 $A D =$ ．

查看试题解析

三、解答题

17. 在 $Δ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $b cos C = (2 a - c) cos B$ ，

(1)、求 $∠ B$ 的大小；

(2)、若 $b = \sqrt{7}$ ， $a + c = 4$ ，求 $a$ ， $c$ 的值.

查看试题解析
18. 已知向量 $\overset{⇀}{a} = (cos x ， - \frac{1}{2})$ ， $\overset{⇀}{b} = (\sqrt{3} sin x ， cos 2 x)$ ， $x \in R$ ，设函数 $f (x) = \overset{⇀}{a} \cdot \overset{⇀}{b}$ .

(1)、求 $f (x)$ 的最小正周期；

(2)、求函数 $f (x)$ 的单调递减区间；

(3)、求 $f (x)$ 在 $[0 ， \frac{π}{2}]$ 上的最大值和最小值.

查看试题解析
19. 据悉，2017年教育机器人全球市场规模已达到8.19亿美元，中国占据全球市场份额10.8%.通过简单随机抽样得到40家中国机器人制造企业，下图是40家企业机器人的产值频率分布直方图.

(1)、求 $m$ 的值；

(2)、在上述抽取的40个企业中任取3个，抽到产值小于500万元的企业不超过两个的概率是多少？

(3)、在上述抽取的40个企业中任取2个，设 $Y$ 为产值不超过500万元的企业个数减去超过500万元的企业个数的差值，求 $Y$ 的分布列及期望.

查看试题解析
20. 如图，某军舰艇位于岛的 $A$ 的正西方 $C$ 处，且与岛的 $A$ 相距12海里.经过侦察发现，国际海盗船以10海里/小时的速度从岛屿 $A$ 出发沿北偏东30°方向逃窜，同时，该军舰艇从 $C$ 处出发沿北偏东 $90 ° - α$ 的方向匀速追赶国际海盗船，恰好用2小时追上.

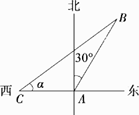(1)、求该军舰艇的速度.

(2)、求 $sin α$ 的值.

查看试题解析
21. 已知函数 $f (x) = \frac{1}{2} x^{2} - 2 a ln x + (a - 2) x$ ， $a \in R$ .

(1)、当 $a = 1$ 时，求函数 $f (x)$ 图象在点 $(1 ， f (1))$ 处的切线方程；

(2)、当 $a < 0$ 时，讨论函数 $f (x)$ 的单调性；

(3)、是否存在实数 $a$ ，对任意 $x_{1}$ ， $x_{2} \in (0 ， + \infty)$ 且 $x_{1} \neq x_{2}$ 有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} > a$ 恒成立？若存在，求出 $a$ 的取值范围；若不存在，说明理由.

查看试题解析
22. 设 $k \in R$ ，函数 $f (x) = ln x - k x$ .

(1)、若 $k = 2$ ， $y = f (x)$ 极大值；

(2)、若 $f (x)$ 无零点，求实数 $k$ 的取值范围；

(3)、若 $f (x)$ 有两个相异零点 $x_{1}$ ， $x_{2}$ ，求证： $ln x_{1} + ln x_{2} > 2$ .

查看试题解析