四川省巴中市2018年中考数学试卷

试卷更新日期：2018-09-27 类型：中考真卷

进入出卷网下载

一、选择题

1. –1+3的结果是（）

A、–4 B、4 C、–2 D、2

查看试题解析
2. 毕业前夕，同学们准备了一份礼物送给自己的母校，现用一个正方体盒子进行包装，六个面上分别写上“祝、母、校、更、美、丽”，其中“祝”与“更”，“母”与“美”在相对的面上．则此包装盒的展开图（不考虑文字方向）不可能是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、a²+a³=a⁵ B、a（b﹣1）=ab﹣a C、3a^﹣¹= $\frac{1}{3 a}$ D、（3a²﹣6a+3）÷3=a²﹣2a

查看试题解析
4. 2017年四川省经济总量达到3.698万亿元，居全国第6位，在全国发展大局中具有重要地位．把3.698万亿用科学记数法表示（精确到0.1万亿）为（）

A、 3.6×10¹² B、3.7×10¹² C、3.6×10¹³ D、3.7×10¹³

查看试题解析
5. 在创建平安校园活动中，九年级一班举行了一次“安全知识竞赛”活动，第一小组6名同学的成绩（单位：分）分别是：87，91，93，87，97，96，下列关于这组数据说正确的是（）

A、中位数是90 B、平均数是90 C、众数是87 D、极差是9

查看试题解析
6. 如图，在△ABC中，点D，E分别是边AC，AB的中点，BD与CE交于点O，连接DE．下列结论：① $\frac{O E}{O B} = \fra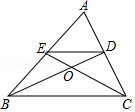c{O D}{O C}$ ；② $\frac{D E}{B C} = \frac{1}{2}$ ；③ $\frac{S_{Δ D O E}}{S_{Δ B O C}} = \frac{1}{2}$ ；④ $\frac{S_{Δ D O E}}{S_{Δ D B E}} = \frac{1}{3}$ ．其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内．已知篮圈中心距离地面高度为3.05m，在如图所示的平面直角坐标系中，下列说法正确的是（）

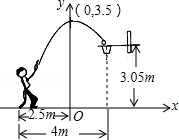A、此抛物线的解析式是y=﹣ $\frac{1}{5}$ x²+3.5 B、篮圈中心的坐标是（4，3.05） C、此抛物线的顶点坐标是（3.5，0） D、篮球出手时离地面的高度是2m

查看试题解析
8. 若分式方程 $\frac{3 x - a}{x^{2} - 2 x} + \frac{1}{x - 2} = \frac{2}{x}$ 有增根，则实数a的取值是（）

A、0或2 B、4 C、8 D、4或8

查看试题解析
9. 如图，⊙O中，半径OC⊥弦AB于点D，点E在⊙O上，∠E=22.5°，AB=4，则半径OB等于（）

A、 $\sqrt{2}$ B、2 C、2 $\sqrt{2}$ D、3

查看试题解析
10. 如图，在Rt△ABC中，∠C=90°，按下列步骤作图：①以点B为圆心，适当长为半径画弧，与AB，BC分别交于点D，E；②分别以D，E为圆心，大于 $\frac{1}{2}$ DE的长为半径画弧，两弧交于点P；③作射线BP交AC于点F；④过点F作FG⊥AB于点G．下列结论正确的是（）

A、CF=FG B、AF=AG C、AF=CF D、AG=FG

查看试题解析

二、填空题

11. 函数y= $\sqrt{x - 1} + \frac{1}{x - 2}$ 中自变量x的取值范围是．

查看试题解析
12. 分解因式：2a³﹣8a= ．

查看试题解析
13. 已知|sinA﹣ $\frac{1}{2}$ |+ $\sqrt{{(\sqrt{3} - tan B)}^{2}}$ =0，那么∠A+∠B= ．

查看试题解析
14. 甲、乙两名运动员进行了5次百米赛跑测试，两人的平均成绩都是13.3秒，而S_甲²=3.7，S_乙²=6.25，则两人中成绩较稳定的是．

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90°，点D、点E分别是边AB、AC的中点，点F在AB上，且EF∥CD．若EF=2，则AB= ．

查看试题解析
16. 如图，在△ABC中，BO、CO分别平分∠ABC、∠ACB．若∠BOC=110°，则∠A= ．

查看试题解析
17. 把抛物线y=x²﹣2x+3沿x轴向右平移2个单位，得到的抛物线解析式为．

查看试题解析
18. 不等式组 ${\begin{matrix} 3 x \leq 2 x - 4 \\ \frac{x - 1}{2} - 1 < x + 1 \end{matrix}$ 的整数解是x= ．

查看试题解析
19. 如图，在矩形ABCD中，以AD为直径的半圆与边BC相切于点E，若AD=4，则图中的阴影部分的面积为．

查看试题解析
20. 对于任意实数a、b，定义：a◆b=a²+ab+b² ．若方程（x◆2）﹣5=0的两根记为m、n，则m²+n²= ．

查看试题解析

三、解答题

21. 计算： $\sqrt{8}$ +（﹣ $\frac{1}{3}$ ）^﹣¹+|1﹣ $\sqrt{2}$ |﹣4sin45°．

查看试题解析
22. 解方程：3x（x﹣2）=x﹣2．

查看试题解析
23. 先化简，再求值： $(\frac{1}{x^{2} - 4} + \frac{1}{x + 2}) \div \frac{x - 1}{x - 2}$ ，其中x=﹣ $\frac{3}{2}$ ．

查看试题解析
24. 如图，在▱ABCD中，过B点作BM⊥AC于点E，交CD于点M，过D点作DN⊥AC于点F，交AB于点N．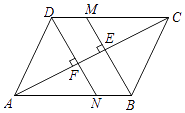

(1)、求证：四边形BMDN是平行四边形；

(2)、已知AF=12，EM=5，求AN的长．

查看试题解析
25. 在如图所示的平面直角坐标系中，已知点A（﹣3，﹣3），点B（﹣1，﹣3），点C（﹣1，﹣1）．

(1)、画出△ABC；

(2)、画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出A₁点的坐标：；

(3)、以O为位似中心，在第一象限内把△ABC扩大到原来的两倍，得到△A₂B₂C₂ ，并写出A₂点的坐标：．

查看试题解析
26. 在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球，把它们充分搅匀．

(1)、“从中任意抽取1个球不是红球就是白球”是事件，“从中任意抽取1个球是黑球”是事件；

(2)、从中任意抽取1个球恰好是红球的概率是；

(3)、学校决定在甲、乙两名同学中选取一名作为学生代表发言，制定如下规则：从盒子中任取两个球，若两球同色，则选甲；若两球异色，则选乙．你认为这个规则公平吗？请用列表法或画树状图法加以说明．

查看试题解析
27. 如图所示，四边形ABCD是菱形，边BC在x轴上，点A（0，4），点B（3，0），双曲线y= $\frac{k}{x}$ 与直线BD交于点D、点E．

(1)、求k的值；

(2)、求直线BD的解析式；

(3)、求△CDE的面积．

查看试题解析
28. 学校需要添置教师办公桌椅A、B两型共200套，已知2套A型桌椅和1套B型桌椅共需2000元，1套A型桌椅和3套B型桌椅共需3000元．

(1)、求A，B两型桌椅的单价；

(2)、若需要A型桌椅不少于120套，B型桌椅不少于70套，平均每套桌椅需要运费10元．设购买A型桌椅x套时，总费用为y元，求y与x的函数关系式，并直接写出x的取值范围；

(3)、求出总费用最少的购置方案．

查看试题解析
29. 在一次课外活动中，甲、乙两位同学测量公园中孔子塑像的高度，他们分别在A，B两处用高度为1.5m的测角仪测得塑像顶部C的仰角分别为30°，45°，两人间的水平距离AB为10m，求塑像的高度CF．（结果保留根号）

查看试题解析
30. 如图，在△ABC中，AB=BC，以AB为直径的⊙O交BC于点D，交AC于点F，过点C作CE∥AB，与过点A的切线相交于点E，连接AD．

(1)、求证：AD=AE；

(2)、若AB=6，AC=4，求AE的长．

查看试题解析
31. 如图，在平面直角坐标系中，抛物线y=ax²+bx﹣2与x轴交于点A、B（点A在点B的左侧），与y轴交于点C（0，﹣2），OB=4OA，tan∠BCO=2．

(1)、求A、B两点的坐标；

(2)、求抛物线的解析式；

(3)、点M、N分别是线段BC、AB上的动点，点M从点B出发以每秒 $\frac{\sqrt{5}}{2}$ 个单位的速度向点C运动，同时点N从点A出发以每秒2个单位的速度向点B运动，当点M、N中的一点到达终点时，两点同时停止运动．过点M作MP⊥x轴于点E，交抛物线于点P．设点M、点N的运动时间为t（s），当t为多少时，△PNE是等腰三角形？

查看试题解析