青海省2018年中考数学试卷
试卷更新日期:2018-09-27 类型:中考真卷
一、填空题
-
1. 的倒数是;4的算术平方根是 .2. 分解因式: ;不等式组 的解集是
3. 近年来,国家重视精准扶贫,收效显著,据统计约65000000人脱贫,65000000用科学记数法可表示为 .
4. 函数 中自变量x的取值范围是 .
5. 如图,直线 ,直线EF与AB、CD相交于点E、F, 的平分线EN与CD相交于点 若 ,则 .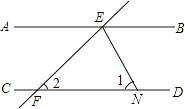 6. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连接AD,若 ,则 .
6. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连接AD,若 ,则 . 7. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 .
7. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 .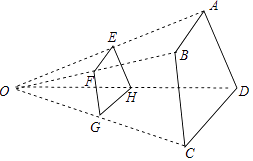 8. 某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图 如图 ,可计算出该店当月销售出水果的平均价格是元
8. 某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图 如图 ,可计算出该店当月销售出水果的平均价格是元 9. 如图,A,B,C是 上的三个点,若 ,则 .
9. 如图,A,B,C是 上的三个点,若 ,则 .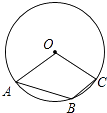 10. 在 中,若 ,则 的度数是 .
10. 在 中,若 ,则 的度数是 .
11. 如图,用一个半径为20cm,面积为 的扇形铁皮,制作一个无底的圆锥 不计接头损耗 ,则圆锥的底面半径r为cm.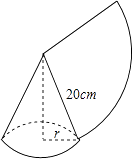 12. 如图,下列图案是由火柴棒按某种规律搭成的,第 个图案中有2个正方形,第 个图案中有5个正方形,第 个图案中有8个正方形 ,则第 个图案中有个正方形,第n个图案中有个正方形.
12. 如图,下列图案是由火柴棒按某种规律搭成的,第 个图案中有2个正方形,第 个图案中有5个正方形,第 个图案中有8个正方形 ,则第 个图案中有个正方形,第n个图案中有个正方形.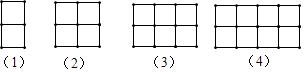
二、单项选择题
-
13. 关于一元二次方程 根的情况,下列说法正确的是( )
A、有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根14. 用扇形统计图反映地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是 ,当宇宙中一块陨石落在地球上,则落在陆地上的概率是( )
A、 B、 C、 D、15. 若 , 是函数 图象上的两点,当 时,下列结论正确的是( )
A、 B、 C、 D、16. 某班举行趣味项目运动会,从商场购买了一定数量的乒乓球拍和羽毛球拍作为奖品 若每副羽毛球拍的价格比乒乓球拍的价格贵6元,且用400元购买乒乓球拍的数量与用550元购买羽毛球拍的数量相同 设每副乒乓球拍的价格为x元,则下列方程正确的是( )
A、 B、 C、 D、17. 由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )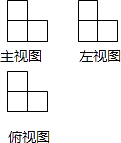 A、3块 B、4块 C、6块 D、9块18. 小桐把一副直角三角尺按如图所示的方式摆放在一起,其中 , , , ,则 等于( )
A、3块 B、4块 C、6块 D、9块18. 小桐把一副直角三角尺按如图所示的方式摆放在一起,其中 , , , ,则 等于( )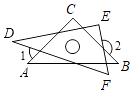 A、 B、 C、 D、19. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )
A、 B、 C、 D、19. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )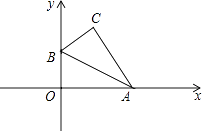 A、 B、 C、 D、20. 均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是
A、 B、 C、 D、20. 均匀地向一个容器注水,最后将容器注满 在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是 A、
A、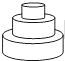 B、
B、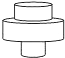 C、
C、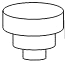 D、
D、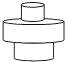
三、解答题
-
21. 先化简,再求值: ,其中 .
22. 计算:
23. 如图,在平行四边形ABCD中,E为AB边上的中点,连接DE并延长,交CB的延长线于点F.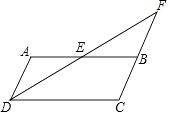 (1)、求证: ;(2)、若平行四边形ABCD的面积为32,试求四边形EBCD的面积.
(1)、求证: ;(2)、若平行四边形ABCD的面积为32,试求四边形EBCD的面积.
24. 如图,同学们利用所学知识去测量三江源某河段某处的宽度 小宇同学在A处观测对岸点C,测得 ,小英同学在距点A处60米远的B点测得 ,请根据这些数据算出河宽 精确到 米, , .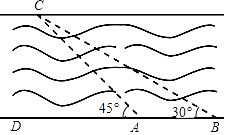 25. 如图 内接于 , ,CD是 的直径,点P是CD延长线上一点,且 .
25. 如图 内接于 , ,CD是 的直径,点P是CD延长线上一点,且 .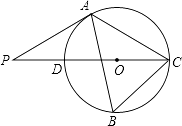 (1)、求证:PA是 的切线;(2)、若 ,求 的直径.26. 某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查 随机调查了某班所有同学最喜欢的节目 每名学生必选且只能选择四类节目中的一类 并将调查结果绘成如下不完整的统计图 根据两图提供的信息,回答下列问题:
(1)、求证:PA是 的切线;(2)、若 ,求 的直径.26. 某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查 随机调查了某班所有同学最喜欢的节目 每名学生必选且只能选择四类节目中的一类 并将调查结果绘成如下不完整的统计图 根据两图提供的信息,回答下列问题: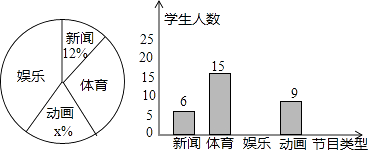 (1)、最喜欢娱乐类节目的有人,图中 ;
(1)、最喜欢娱乐类节目的有人,图中 ;
(2)、请补全条形统计图;
(3)、根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;(4)、在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.27. 请认真阅读下面的数学小探究系列,完成所提出的问题: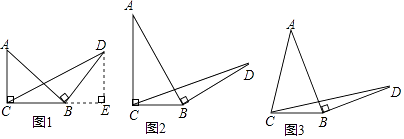 (1)、探究1:如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 求证: 的面积为 提示:过点D作BC边上的高DE,可证 ≌
(1)、探究1:如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 求证: 的面积为 提示:过点D作BC边上的高DE,可证 ≌
(2)、探究2:如图2,在一般的 中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 请用含a的式子表示 的面积,并说明理由.
(3)、探究3:如图3,在等腰三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 试探究用含a的式子表示 的面积,要有探究过程.28. 如图,抛物线 与坐标轴交点分别为 , , ,作直线BC.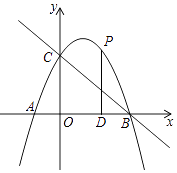 (1)、求抛物线的解析式;(2)、点P为抛物线上第一象限内一动点,过点P作 轴于点D,设点P的横坐标为 ,求 的面积S与t的函数关系式;(3)、条件同 ,若 与 相似,求点P的坐标.
(1)、求抛物线的解析式;(2)、点P为抛物线上第一象限内一动点,过点P作 轴于点D,设点P的横坐标为 ,求 的面积S与t的函数关系式;(3)、条件同 ,若 与 相似,求点P的坐标.