2018-2019学年数学沪科版九年级上册22.3 相似三角形的性质(2) 同步练习
试卷更新日期:2018-09-27 类型:同步测试
一、选择题
-
1. 将直角三角形的三条边长同时扩大同一倍数,得到的三角形是( )A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形2. 如图,△ABC, AB=12,AC=15,D为AB上一点,且AD= AB , 在AC上取一点E, 使以A,D,E为顶点的三角形与ABC相似,则AE等于( )
 A、 B、10 C、 或10 D、以上答案都不对3. 如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( )
A、 B、10 C、 或10 D、以上答案都不对3. 如图,△ABC中,D、E分别为边AB、AC上的点,且DE∥BC,下列判断错误的是( ) A、= B、= C、= D、=4. 等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有( )①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.A、1个 B、2个 C、3个 D、4个5. 如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( )
A、= B、= C、= D、=4. 等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有( )①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.A、1个 B、2个 C、3个 D、4个5. 如图,在△ABC中,EF∥BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( ) A、16 B、18 C、20 D、246. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A、16 B、18 C、20 D、246. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( ) A、 = B、 = C、 = D、 =7. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A、 = B、 = C、 = D、 =7. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )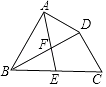 A、 B、 C、 D、8. 如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )。
A、 B、 C、 D、8. 如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )。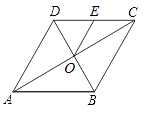 A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题
-
9. 如图,已知AB∥CD,若 = ,则 = .
 10. 已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .
10. 已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 . 11. 如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=cm.
11. 如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=cm. 12. 如图,在直角 中, , AC=6, BC=8, P、 Q分别为边 BC、 AB上的两个动点,若要使 是等腰三角形且 是直角三角形,则 AQ= .
12. 如图,在直角 中, , AC=6, BC=8, P、 Q分别为边 BC、 AB上的两个动点,若要使 是等腰三角形且 是直角三角形,则 AQ= . 13. 如图,在▱ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= .
13. 如图,在▱ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= . 14. 如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为 .
14. 如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为 . 15. 如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM= ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 .
15. 如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM= ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 .
三、解答题
-
16. 已知:如图,在 中,D是AC上一点,联结BD,且∠ABD =∠ACB.
 (1)、求证:△ABD∽△ACB;(2)、若AD=5,AB= 7,求AC的长.17. 如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.若AB=6,AD=12,BE=8,求:DF的长,以及四边形DCEF的面积。
(1)、求证:△ABD∽△ACB;(2)、若AD=5,AB= 7,求AC的长.17. 如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.若AB=6,AD=12,BE=8,求:DF的长,以及四边形DCEF的面积。 18. 如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即 ,BE交DC于点F,已知 ,求CF的长 .
18. 如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即 ,BE交DC于点F,已知 ,求CF的长 . 19. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
19. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.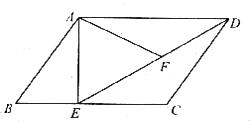 (1)、求证:△ADF∽△DEC:(2)、若AB=4,AD=3 ,AE=3,求AF的长.
(1)、求证:△ADF∽△DEC:(2)、若AB=4,AD=3 ,AE=3,求AF的长.

