2018-2019学年数学沪科版九年级上册22.3 相似三角形的性质（1） 同步练习
试卷更新日期：2018-09-27 类型：同步测试
一、选择题
-
1. △ABC中，AB=12，BC=18，CA=24，另一个和它相似的三角形最长的一边是36，则最短的一边是（ ）A、27 B、12 C、18 D、202. 已知△ABC与△DEF相似且面积比为4：1，则△ABC与△DEF的对应边上的高之比为（ ）A、4：1 B、1：4 C、16：1 D、2：13. 相似三角形的最短边分别是5cm和3cm，它们的面积之差为 ，那么小三角形的面积为（ ）
A、 B、 C、 D、4. 如图，△ABC∽△DEF ， 相似比为1：2．若BC=1，则EF的长是（ ）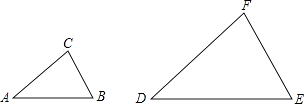
A、1 B、2 C、3 D、45. 若△ABC∽△A′B′C′，相似比为1：2，则△ABC与△A′B′C′的面积的比为（ ）A、1：2 B、2：1 C、1：4 D、4：16. 一个三角形三边之比为3：5：7，与它相似的三角形的最长边为21cm，则其余两边之和为（ ）A、24cm B、21cm C、13cm D、9cm7. 如图，△ABC中，点D在线段BC上，且△ABC∽△DBA，则下列结论一定正确的是（ ）
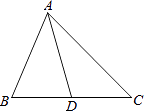A、 B、 C、 D、8. 如果两个相似三角形对应角平分线的比为16：25，那么它们的面积比为（ ）A、4：5 B、16：25 C、196：225 D、256：625二、填空题
-
9. 已知△ABC∽△DEF，△ABC与△DEF的相似比为4：1，则△ABC与△DEF对应边上的高之比为 ．
10. 如图，已知△ABC∽△DEF，且相似比为k，则k= ， 直线y=kx+k的图象必经过象限．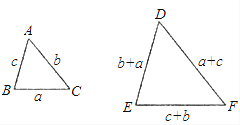
11. 已知△ABC∽△A′B′C′，∠A=50°，则∠A的对应角∠A′=度．
12. 两个三角形相似，其中一个三角形的两个内角是40°、60°．那么另一个三角形的最大角是度，最小角是度．
13. 如图，矩形ABCD两邻边分别为3、4，点P是矩形一边上任意一点，则点P到两条对角线AC、BD的距离之和PE+PF为.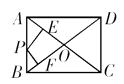
14. 矩形ABCD中，AB=6，BC=8.点P在矩形ABCD的内部，点E在边BC上，满足△PBE∽△DBC，若△APD是等腰三角形，则PE的长为数.
15. 如图，△ABC中，AB=8厘米，AC=16厘米，点P从A出发，以每秒2厘米的速度向B运动，点Q从C同时出发，以每秒3厘米的速度向A运动，其中一个动点到端点时，另一个动点也相应停止运动，那么，当以A、P、Q为顶点的三角形与△ABC相似时，运动时间为
三、解答题
-
16. 两个相似三角形一组对应边的长分别是24cm和12cm，若它们周长的和是240cm，求这两个三角形的周长．
17. 如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE∽△DEF，AB=6，AE=9，DE=2，求EF的长．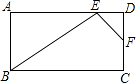
18. 如图，已知△ABC中，AB=8，BC=7，AC=6，点D、E分别在AB、AC上，如果以A、D、E为顶点的三角形和△ABC相似，且相似比为 ，试求AD、AE的长．
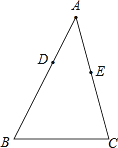19. 已知：如图，△ABC∽△ADE ， AE：EC=5：3，BC=6cm，∠A=40°，∠C=45°．
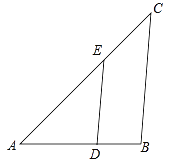(1)、求∠ADE的大小；(2)、求DE的长．20. 如图，点D、E分别在△ABC的边AB、AC上，且AB=9，AC=6，AD=3，若使△ADE与△ABC相似，求AE的长．
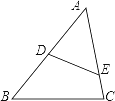21. 如图
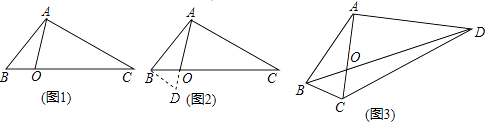(1)、某学校“智慧方园”数学社团遇到这样一个题目：如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO= ，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB=°，AB= ．
(2)、请参考以上解决思路，解决问题：如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO= ，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．