2018-2019学年数学沪科版九年级上册22.2 相似三角形的判定(2) 同步练习
试卷更新日期:2018-09-27 类型:同步测试
一、选择题
-
1. 下列说法中,不正确的是( )A、直角边长分别是6、4和4.5、3的两个直角三角形相似 B、底角为40°的两个等腰三角形相似 C、一个锐角为30°的两个直角三角形相似 D、有个角为30°的两个等腰三角形相似2. 如图,在△ABC中,点D、E分别在边AB、AC上,且DE不行于BC,则下列条件中不能判断△ABC∽△ADE的是( )

A、∠AED=∠B B、∠ADE=∠C C、 = D、 =3. 如图,△ACD和△ABC相似需具备的条件是( )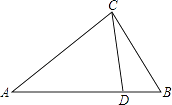 A、 B、 C、AC2=AD•AB D、CD2=AD•BD4. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A、 B、 C、AC2=AD•AB D、CD2=AD•BD4. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )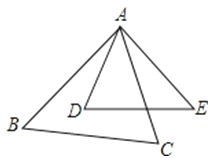 A、= B、= C、= D、=5. 如图,D是△ABC的边AB上的一点,那么下列四个条件不能单独判定△ABC∽△ACD的是( )
A、= B、= C、= D、=5. 如图,D是△ABC的边AB上的一点,那么下列四个条件不能单独判定△ABC∽△ACD的是( )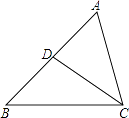 A、∠B=∠ACD B、∠ADC=∠ACB C、 D、AC2=AD•AB6. 下列命题中正确的有( )
A、∠B=∠ACD B、∠ADC=∠ACB C、 D、AC2=AD•AB6. 下列命题中正确的有( )①有一个角等于80°的两个等腰三角形相似;②两边对应成比例的两个等腰三角形相似;③有一个角对应相等的两个等腰三角形相似;④底边对应相等的两个等腰三角形相似.
A、0个 B、1个 C、2个 D、3个7. 下列各组条件中,一定能推得△ABC与△DEF相似的是( )A、∠A=∠E且∠D=∠F B、∠A=∠B且∠D=∠F C、∠A=∠E且 D、∠A=∠E且8. 如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( ) A、
A、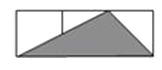 B、
B、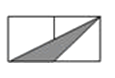 C、
C、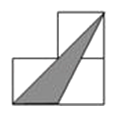 D、
D、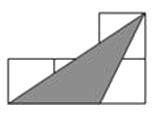
二、填空题
-
9. 如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个)
 10. 已知:△ABC中,点E是AB边的中点,点F在AC边上,若以A,E,F为顶点的三角形与△ABC相似,则需要增加的一个条件是 . (写出一个即可)
10. 已知:△ABC中,点E是AB边的中点,点F在AC边上,若以A,E,F为顶点的三角形与△ABC相似,则需要增加的一个条件是 . (写出一个即可)
11. 如图,在边长为1的正方形网格中有点P、A、B、C,则图中所形成的三角形中,相似的三角形是.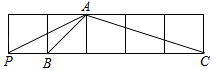 12. 如图,有下列条件:①∠B=∠C;②∠ADB=∠AEC;③ ;④ ;⑤ ,其中一个条件就能使△BPE∽△CPD的条件有个,它们分别是.(只填写序号)
12. 如图,有下列条件:①∠B=∠C;②∠ADB=∠AEC;③ ;④ ;⑤ ,其中一个条件就能使△BPE∽△CPD的条件有个,它们分别是.(只填写序号) 13. 如图,D、E分别是△ABC的边AB、AC上的点,则使△AED∽△ABC的条件是.
13. 如图,D、E分别是△ABC的边AB、AC上的点,则使△AED∽△ABC的条件是.
三、解答题
-
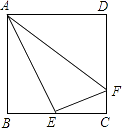
14. 如图,在正方形ABCD中,E为BC的中点,F是DC上的点,且DF=3FC,试说明:△ABE∽△ECF.
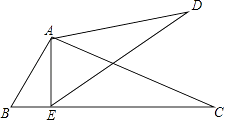
 15. 如图,已知:∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.
15. 如图,已知:∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ABC∽△AED.
 16. 如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:
16. 如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证: (1)、∠OAE=∠OBE;(2)、AE=BE+ OE.17. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= DC,连接EF并延长交BC的延长线于点G.
(1)、∠OAE=∠OBE;(2)、AE=BE+ OE.17. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= DC,连接EF并延长交BC的延长线于点G. (1)、求证:△ABE∽△DEF;(2)、若正方形的边长为4,求BG的长.18. 如图,在矩形ABCD中,AB=18cm,AD=9cm,点M沿AB边从A点开始向B以2cm/s的速度移动,点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求:
(1)、求证:△ABE∽△DEF;(2)、若正方形的边长为4,求BG的长.18. 如图,在矩形ABCD中,AB=18cm,AD=9cm,点M沿AB边从A点开始向B以2cm/s的速度移动,点N沿DA边从D点开始向A以1cm/s的速度移动.如果点M、N同时出发,用t(s)表示移动时间(0≤t≤9),求: (1)、当t为何值时,∠ANM=45°?
(1)、当t为何值时,∠ANM=45°?
(2)、计算四边形AMCN的面积,根据计算结果提出一个你认为合理的结论;
(3)、当t为何值时,以点M、N、A为顶点的三角形与△BCD相似?