2018-2019学年数学沪科版九年级上册22.2 相似三角形的判定(1) 同步练习
试卷更新日期:2018-09-27 类型:同步测试
一、选择题
-
1. 如图,在平行四边形ABCD中,P为对角线AC上一点,过点P作AB的平行线,分别与AD,BC相交于E,F,则图中与△AEP相似的三角形有( )
 A、1个 B、2个 C、3个 D、4个2. 如图所示,△ABC中,CD⊥AB于D,DE⊥AC于E,图中与△ADE相似的三角形有( )个.
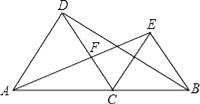
A、1个 B、2个 C、3个 D、4个2. 如图所示,△ABC中,CD⊥AB于D,DE⊥AC于E,图中与△ADE相似的三角形有( )个. A、1 B、2 C、3 D、43. 如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,BC分别与AD,AE相交于点F,G.图中共有n对三角形相似(相似比不等于1),则n的值是( )
A、1 B、2 C、3 D、43. 如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,BC分别与AD,AE相交于点F,G.图中共有n对三角形相似(相似比不等于1),则n的值是( ) A、2 B、3 C、4 D、54. 如图,△ABC中,D,E分别为AB,AC上的点,如果∠1=∠2=∠3,那么图中的相似三角形共有( )对.
A、2 B、3 C、4 D、54. 如图,△ABC中,D,E分别为AB,AC上的点,如果∠1=∠2=∠3,那么图中的相似三角形共有( )对.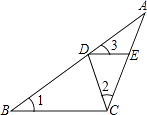 A、2 B、3 C、4 D、55. 如图,在等腰梯形ABCD中,AD∥BC,过点C作CE∥AB,P是梯形ABCD内一点,连接BP并延长交CD于点F,交CE于点E,再连接PC,已知BP=PC,则下列结论错误的是( )
A、2 B、3 C、4 D、55. 如图,在等腰梯形ABCD中,AD∥BC,过点C作CE∥AB,P是梯形ABCD内一点,连接BP并延长交CD于点F,交CE于点E,再连接PC,已知BP=PC,则下列结论错误的是( ) A、∠1=∠2 B、∠2=∠E C、△PFC∽△PCE D、△EFC∽△ECB6. 如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )
A、∠1=∠2 B、∠2=∠E C、△PFC∽△PCE D、△EFC∽△ECB6. 如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( ) A、△ADE∽△ABC B、△ADE∽△ACD C、△ADE∽△DCB D、△DEC∽△CDB7.
A、△ADE∽△ABC B、△ADE∽△ACD C、△ADE∽△DCB D、△DEC∽△CDB7.在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
 A、一定相似 B、当E是AC中点时相似 C、不一定相似 D、无法判断8. 在△ABC中,∠A>∠B>∠C,∠A≠90°,画直线使它把△ABC分成两部分,且使其中一部分与△ABC相似,这样的互不平行的直线有( )条.
A、一定相似 B、当E是AC中点时相似 C、不一定相似 D、无法判断8. 在△ABC中,∠A>∠B>∠C,∠A≠90°,画直线使它把△ABC分成两部分,且使其中一部分与△ABC相似,这样的互不平行的直线有( )条.
A、3 B、4 C、5 D、6二、填空题
-
9. 如图,在△ABC中点D、E分别在边AB、AC上,请添加一个条件: , 使△ABC∽△AED.
 10. 如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽ , △BAD∽△ACD(写出一个三角形即可).
10. 如图,在△ABC中,∠BAC=90°,∠B=30°,AD⊥BC,AE平分∠BAD,则△ABC∽ , △BAD∽△ACD(写出一个三角形即可).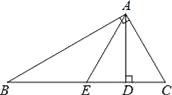 11. 如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 . (只需写一个条件,不添加辅助线和字母)
11. 如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 . (只需写一个条件,不添加辅助线和字母)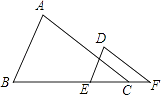 12. 如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN= .
12. 如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN= . 13. 过△ABC(AB>AC)的边AC边上一定点M作直线与AB相交,使得到的新三角形与△ABC相似,这样的直线共有条.
13. 过△ABC(AB>AC)的边AC边上一定点M作直线与AB相交,使得到的新三角形与△ABC相似,这样的直线共有条.
14. 如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D,与AB及AC的延长线分别交于E,F,写出图中的一对全等三角形是;一对相似三角形是 .
三、解答题
-
15. 已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.
 16. 在矩形ABCD中,F是BC上一点,AF的延长线交DC的延长线于G,DE⊥AG于E.根据上述条件,请在图中找出四组相似三角形,并说明其中一组的理由.
16. 在矩形ABCD中,F是BC上一点,AF的延长线交DC的延长线于G,DE⊥AG于E.根据上述条件,请在图中找出四组相似三角形,并说明其中一组的理由. 17. 如图,在△ABC中,∠BAC=90°,M是BC的中点,过点A作AM的垂线,交CB的延长线于点D.求证:△DBA∽△DAC.
17. 如图,在△ABC中,∠BAC=90°,M是BC的中点,过点A作AM的垂线,交CB的延长线于点D.求证:△DBA∽△DAC.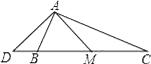 18. 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
18. 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.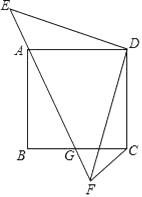
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.