广东省汕头市潮南区2018届数学中考模拟试卷

试卷更新日期：2018-09-27 类型：中考模拟

进入出卷网下载

一、单选题

1. |﹣3|的值是（）

A、3 B、 $\frac{1}{3}$ C、﹣3 D、﹣ $\frac{1}{3}$

查看试题解析
2. 下列图形中既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、2⁰=0 B、 $\sqrt{4}$ =±2 C、2^﹣1= $\frac{1}{2}$ D、2³=6

查看试题解析
4. 一个五边形的5个内角中，钝角至少有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
5. 2015年5月31日，我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中，获得好成绩，成为历史上首位突破10秒大关的黄种人，如表是苏炳添近五次大赛参赛情况：则苏炳添这五次比赛成绩的众数和中位数分别为（）
比赛日期
2012﹣8﹣4
2013﹣5﹣21
2014﹣9﹣28
2015﹣5﹣20
2015﹣5﹣31
比赛地点
英国伦敦
中国北京
韩国仁川
中国北京
美国尤金
成绩（秒）
10.19
10.06
10.10
10.06
9.99

A、10.06秒，10.06秒 B、10.10秒，10.06秒 C、10.06秒，10.10秒 D、10.08秒，10.06秒

查看试题解析
6. 据悉，超级磁力风力发电机可以大幅度提升风力发电效率，但其造价高昂，每座磁力风力发电机，其建造花费估计要5 300万美元，“5 300万”用科学记数法可表示为（）

A、5.3×10³ B、5.3×10⁴ C、5.3×10⁷ D、5.3×10⁸

查看试题解析
7. 如图所示，已知AB∥CD，AD∥BC，AC与BD交于点O，AE⊥BD于E，CF⊥BD于E，图中全等三角形有（）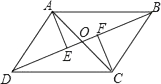

A、3对 B、5对 C、6对 D、7对

查看试题解析
8. 如图，矩形ABCD中，AB=5，AD=12，将矩形ABCD按如图所示的方式在直线l上进行两次旋转，则点B在两次旋转过程中经过的路径的长是（）

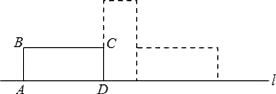A、 $\frac{25}{2} π$ B、13π C、25π D、25 $\sqrt{2}$

查看试题解析
9. 若分式 $\frac{x^{2} - 9}{x - 3}$ 的值为0，则x的值等于（）

A、0 B、±3 C、3 D、﹣3

查看试题解析
10. 如图，正方形ABCD中，点E在边BC上，且CE=2BE．连接BD、DE、AE，且AE交BD于F，OG为△BDE的中位线．下列结论：①OG⊥CD；②AB=5OG；③ $\frac{S_{△ O D G}}{S_{△ A B E}} = \frac{1}{3}$ ；④BF=OF；⑤ $cos ∠ B F E = \frac{\sqrt{5}}{5}$ ，其中正确结论的个数是（）

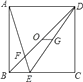A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 若x，y为实数，y= $\frac{\sqrt{x^{2} - 4} + \sqrt{4 - x^{2}} + 1}{x - 2}$ ，则4y﹣3x的平方根是．

查看试题解析
12. 如图，△ABC中，∠BAC=75°，BC=7，△ABC的面积为14，D为 BC边上一动点（不与B，C重合），将△ABD和△ACD分别沿直线AB，AC翻折得到△ABE与△ACF，那么△AEF的面积最小值为．

查看试题解析
13. 已知 $\sqrt{2 a + b^{2}} + | b - 4 | = 0$ ，则a+b=

查看试题解析
14. 如图所示方格纸中每个小正方形的边长为1，其中有三个格点A、B、C，则sin∠ABC= ．

查看试题解析
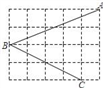15. 抛物线y=﹣2x²+6x﹣1的顶点坐标为。

查看试题解析
16. 如图，⊙O的直径AB的长12，长度为4的弦DF在半圆上滑动，DE⊥AB于点E，OC⊥DF于点C，连接CE，AF，则sin∠AEC的值是，当CE的长取得最大值时AF的长是．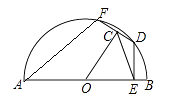

查看试题解析

三、解答题

17. 已知关于x，y的不等式组 ${\begin{matrix} x + k \leq 5 - 2 x \\ 4 (x - \frac{3}{4}) \geq x - 1 \end{matrix}$ ，

(1)、若该不等式组的解为 $\frac{2}{3} \leq x \leq 3$ ，求k的值；

(2)、若该不等式组的解中整数只有1和2，求k的取值范围．

查看试题解析
18. 先化简，再求值： $(a - 1 + \frac{2}{a + 1}) \div (a^{2} + 1)$ ，其中 $a = \sqrt{2} - 1$ ．

查看试题解析
19. 如图所示，在∠BAC中

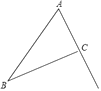(1)、利用尺规按下列要求作图，作∠BAC的平分线与线段BC的垂直平分线的交点D，过点D分别作线段DE⊥AB于点E、线段DF⊥AC于点F．（不写作法，保留作图痕迹）

(2)、求证：BE=CF．

(3)、求证：AB+AC=2AF．

查看试题解析
20. 如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是α，然后在水平地面上向建筑物前进了m米，此时自B处测得建筑物顶部的仰角是β．已知测角仪的高度是n米，请你计算出该建筑物的高度．

查看试题解析
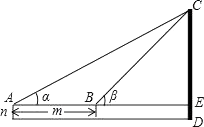21. 2013年5月31日是第26个“世界无烟日”，校学生会书记小明同学就“戒烟方式”的了解程度对本校九年级学生进行了一次随机问卷调查，如图是他采集数据后绘制的两幅不完整的统计图（A：了解较多，B：不了解，C：了解一点，D：非常了解）．请你根据图中提供的信息解答以下问题：

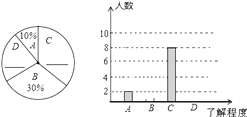(1)、在扇形统计图中的横线上填写缺失的数据，并把条形统计图补充完整．

(2)、2013年该初中九年级共有学生400人，按此调查，可以估计2013年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人？

(3)、在问卷调查中，选择“A”的是1名男生，1名女生，选择“D”的有4人且有2男2女．校学生会要从选择“A、D”的问卷中，分别抽一名学生参加活动，请你用列表法或树状图求出恰好是一名男生一名女生的概率．

查看试题解析
22. 甲、乙两支“徒步队”到野外沿相同路线徒步，徒步的路程为24千米．甲队步行速度为4千米/时，乙队步行速度为6千米/时．甲队出发1小时后，乙队才出发，同时乙队派一名联络员跑步在两队之间来回进行一次联络（不停顿），他跑步的速度为10千米/时．

(1)、乙队追上甲队需要多长时间？

(2)、联络员从出发到与甲队联系上后返回乙队时，他跑步的总路程是多少？

(3)、从甲队出发开始到乙队完成徒步路程时止，何时两队间间隔的路程为1千米？

查看试题解析
23. 某中学开学初到商场购买A、B两种品牌的足球，购买A种品牌的足球20个，B种品牌的足球30个，共花费4600元，已知购买4个B种品牌的足球与购买5个A种品牌的足球费用相同．

(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元．

(2)、学校为了响应习总书记“足球进校园”的号召，决定再次购进A、B两种品牌足球共42个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高5元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的80%，且保证这次购买的B种品牌足球不少于20个，则这次学校有哪几种购买方案？

(3)、请你求出学校在第二次购买活动中最多需要多少资金？

查看试题解析
24. 如图，已知AB是⊙O的直径，弦CD与AB交于点E，F为CD的延长线上一点，连接AF，且FA²=FD•FC．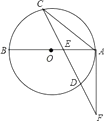

(1)、求证：FA为⊙O的切线；

(2)、若AC=8，CE：ED=6：5，AE：EB=2：3，求AB的值．

查看试题解析
25. 如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：

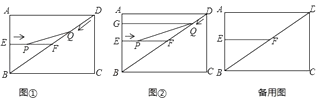(1)、求证：△BEF∽△DCB；

(2)、当点Q在线段DF上运动时，若△PQF的面积为0.6cm² ，求t的值；

(3)、当t为何值时，△PQF为等腰三角形？试说明理由．

查看试题解析

比赛日期	2012﹣8﹣4	2013﹣5﹣21	2014﹣9﹣28	2015﹣5﹣20	2015﹣5﹣31
比赛地点	英国伦敦	中国北京	韩国仁川	中国北京	美国尤金
成绩（秒）	10.19	10.06	10.10	10.06	9.99