广东省汕头市潮南区2018届初中毕业生学业考试模拟考试数学试卷
试卷更新日期：2018-09-27 类型：中考模拟
一、单选题
-
1. ﹣5的倒数是（ ）A、 B、±5 C、5 D、﹣2. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）A、
B、
C、
D、
3. 某商品的标价为200元，8折销售仍赚40元，则商品进价为（ ）元．A、140 B、120 C、160 D、1004. 已知一组数据：3，4，6，7，8，8，下列说法正确的是（ ）A、众数是2 B、众数是8 C、中位数是6 D、中位数是75.如图，a∥b，∠1=∠2，∠3=40°，则∠4等于（ ）
A、40° B、50° C、60° D、70°6. 2017年广东汕头GDP总量超过2300亿人民币，2300亿用科学记数法表示为（ ）A、 0.23×1011 B、2.3×1010 C、2.3×1011 D、0.23×10127.如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（ ）
A、6 米 B、6米 C、3 米 D、3米8. 实数a，b在数轴上对应点的位置如图所示，化简|a|+ 的结果是（ ）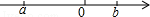
A、﹣2a+b B、2a﹣b C、﹣b D、b9. 如图，CB＝CA，∠ACB＝90°，点D在边BC上(与B，C不重合)，四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC＝FG；②S△FAB∶S四边形CBFG＝1∶2；③∠ABC＝∠ABF；④AD2＝FQ·AC，其中正确结论的个数是（ ）
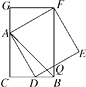A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 分解因式：2x2-4x+2= ．11. 函数y= 中，自变量x的取值范围是 ．12. 正八边形一个内角的度数为 ．13. 如图，在四边形ABCD中，E、F分别是AB、AD的中点，若EF=4，BC=10，CD=6，则tanC=
14. 如图，已知OB=1，以OB为直角边作等腰直角三角形A1BO，再以OA1为直角边作等腰直角三角形A2A1O，如此下去，则线段OAn的长度为 ．
三、解答题、
-
15. 定义运算“※”，规定x※y＝ax2＋by，其中a，b为常数，且1※2＝5，2※1＝6，则2※3＝ ．16. 计算：| ﹣2|+2sin60°+ ﹣ ．17. 先化简，再求值：（ ）÷ ．其中a=-118. 如图，已知在△ABC中，AB=AC．
(1)、试用直尺和圆规在AC上找一点D，使AD=BD（不写作法，但需保留作图痕迹）．(2)、在（1）中，连接BD，若BD=BC，求∠A的度数．19. 某中学组织七、八、九年级学生参加全区作文比赛，该校将收到的参赛作文进行分年级统计，绘制了如图1和如图2两幅不完整的统计图，根据图中提供的信息完成以下问题．
(1)、此次参赛的作文篇数共有篇；(2)、扇形统计图中九年级参赛作文篇数对应的圆心角是度，并补全条形统计图；(3)、经过评审，全校有4篇作文荣获特等奖，其中有一篇来自七年级，学校准备从特等奖作文中任选两篇刊登在校刊上，请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率．20. 如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．
(1)、求证：△AED≌△CFB；(2)、若∠A=30°，∠DEB=45°，求证：DA=DF．21. 如图，在平面直角坐标系中，一次函数y=mx+n（m≠0）的图象与反比例函数y= （k≠0）的图象交于第一、三象限内的A、B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为M，BM=OM，OB=2 ，点A的纵坐标为4．
(1)、求该反比例函数和一次函数的解析式；(2)、连接MC，求四边形MBOC的面积．22. 如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB.
(1)、求证：PC是⊙O的切线；(2)、求证：BC= AB；(3)、点M是弧AB的中点，CM交AB于点N，若AB=4，求MN
MC的值. 23. 正方形ABCD的边长为6cm，点E，M分别是线段BD，AD上的动点，连接AE并延长，交边BC于F，过M作MN⊥AF，垂足为H，交边AB于点N.
(1)、如图①，若点M与点D重合，求证：AF＝MN；(2)、如图②，若点M从点D出发，以1cm/s的速度沿DA向点A运动，同时点E从点B出发，以 cm/s的速度沿BD向点D运动，运动时间为ts.①设BF＝ycm，求y关于t的函数表达式；
②当BN＝2AN时，连接FN，求FN的长．