黑龙江省大庆杜蒙县2016-2017学年七年级上学期数学第一次月考试卷
试卷更新日期:2018-09-26 类型:月考试卷
一、单选题
-
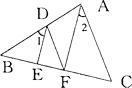
1. 代数式 是( )A、多项式 B、三次多项式 C、三次三项式 D、四次三项式2. 下列计算结果正确的是( )A、 B、 = C、 D、3. 下列算式能用平方差公式计算的是( )A、 B、 C、 D、4. 计算: 的结果等于( )A、 B、 C、 D、5. 如果一个角的两边分别平行于另一个角的两边,那么这两个角( )A、相等 B、互补 C、相等或互补 D、以上结论都不对6. 如下图,如果∠AFE+∠FED=180°,那么( )
 A、AC∥DE B、AB∥FE C、ED⊥AB D、EF⊥AC7. 下列说法中,为平行线特征的是( )
A、AC∥DE B、AB∥FE C、ED⊥AB D、EF⊥AC7. 下列说法中,为平行线特征的是( )①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.
A、① B、②③ C、④ D、②和④8. 已知 则 ( )A、 B、50 C、500 D、无法计算9. 如果 (x−2)(x+3)=x2+mx+n,那么m、n的值分别是 ( )
A、5,6 B、1,-6 C、-1,6 D、5,-610. 若正方形的边长增加3cm,它的面积就增加39cm,则正方形的边长原来是( )
A、8cm B、6cm C、5cm D、10cm二、填空题
-
11. 单项式 的系数是 , 次数是 .12. 计算 , = .13. 已知 ,则 .14. 如果 是一个完全平方式,那么m的值 .15. 用科学记数法表示:0.0000025= , -1490000000= .16. 如图,若l1∥l2 , ∠1=45°,则∠2=.
 17. 如果 , 那么 .
17. 如果 , 那么 .
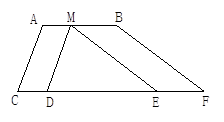
18. 如图,DAE在同一直线上,DE∥BC,则∠BAC= . 19. 如图,已知l1∥l2 , ∠1=40°,∠2=55°,则∠3= , ∠4= .
19. 如图,已知l1∥l2 , ∠1=40°,∠2=55°,则∠3= , ∠4= . 20. 一个角的余角与这个角的补角也互为补角,这个角等于度.
20. 一个角的余角与这个角的补角也互为补角,这个角等于度.
21. 如图1所示,边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形。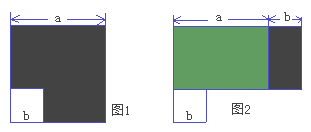 (1)、请你分别表示出这两个图形中阴影部分的面积: , ;(2)、请问以上结果可以验证哪个乘法公式? ;(3)、试利用这个公式计算:
(1)、请你分别表示出这两个图形中阴影部分的面积: , ;(2)、请问以上结果可以验证哪个乘法公式? ;(3)、试利用这个公式计算:①、 ②、
③、
三、解答题
-
22.(1)、(2)、(3)、(4)、(5)、(6)、23. 化简并求值 ,其中 .24. 计算 .25. 推理填空:
已知:如图AB⊥BC于B,CD⊥BC于C,∠1=∠2,求证:BE∥CF.

证明:∵ AB⊥BC于B,CO⊥BC于C ( 已知 )
∴∠1+∠3=90°,∠2+∠4=90°
∴∠1与∠3互余,∠2与∠4互余
又∵∠1=∠2() ,
∴=()
∴BE∥CF() .
26. 已知 ,求代数式 的值.