浙江省杭州市萧山区瓜沥片2017届九年级上学期数学12月月考试卷

试卷更新日期：2018-09-26 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知 $\frac{a}{b}$ = $\frac{1}{3}$ ，则 $\frac{b - a}{b}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 一个不透明口袋中装有3个红球2个白球，除颜色外都相同，从中任意摸出一个球，下列叙述正确的是（　　）

A、摸到红球是必然事件 B、摸到白球是不可能事件 C、摸到红球的可能性比白球大 D、摸到白球的可能性比红球大

查看试题解析
3. 已知（﹣1，y₁），（﹣2，y₂），（﹣4，y₃）是抛物线y=﹣2x²﹣8x+m上的点，则（　　）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₃＜y₁＜y₂ D、y₂＜y₃＜y₁

查看试题解析
4. 对于抛物线y=（x+1）²+3有以下结论：①抛物线开口向下；②对称轴为直线x=1；③顶点坐标为（﹣1，3）；④x＞1时，y随x的增大而减小．其中正确结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 设二次函数y=（x﹣3）²﹣4图象的对称轴为直线l，若点M在直线l上，则点M的坐标可能是（）

A、（1，0） B、（3，0） C、（﹣3，0） D、（0，﹣4）

查看试题解析
6. 如图，在△ABC中，AB=AC，DE∥BC，则下列结论中不正确的是（）

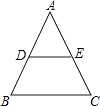A、AD=AE B、DB=EC C、∠ADE=∠C D、DE= $\frac{1}{2}$ BC

查看试题解析
7. 已知⊙O的半径为2cm，弦AB长为2cm，则这条弦的中点到弦所对优弧中点的距离为（）

A、2cm B、 $\sqrt{3}$ cm C、(2－ $\sqrt{3}$ )cm D、(2＋ $\sqrt{3}$ )cm

查看试题解析
8. 下列命题中，其中正确的命题个数有（）
（ 1 ）已知⊙O的半径为1，AB是⊙O的一条弦，AB= $\sqrt{3}$ ，则弦AB所对圆周角的度数为60度；（2）已知⊙O的半径为5，圆心O到弦AB的距离为3，则⊙O上到弦AB所在直线的距离为2的点有3个；（3）平分弦的直径垂直于弦；（4）已知点P是线段AB的黄金分割点，若AB=1，AP= $\frac{\sqrt{5} - 1}{2}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知：如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在 $\overset{⌢}{A B}$ 上的点D处，折痕交OA于点C，则 $\overset{⌢}{A D}$ 的长为（）

A、2π B、3π C、4π D、5π

查看试题解析
10. 若实数m满足 $m^{2} + 2 (1 + \frac{2}{m}) = 0$ ，则下列对m值的估计正确的是（）

A、-2＜m＜-1 B、-1＜m＜0 C、0＜m＜1 D、1＜m＜2

查看试题解析

二、填空题

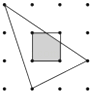
11. 若a=2，b=8，那么a和b的比例中项为。

查看试题解析
12. 将抛物线 $y = - x^{2}$ 先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为．

查看试题解析
13. 在一个不透明的箱子里装有红色、蓝色、黄色的球共20个，除颜色外，形状、大小、质地等完全相同，小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在10%和15%，则箱子里蓝色球的个数很可能是个．

查看试题解析
14. 若圆O的直径AB为2，弦AC为 $\sqrt{2}$ ，弦AD为 $\sqrt{3}$ ，则 $S_{扇形 O C D}$ （其中 $2 S_{扇形 O C D} < S_{圆 O}$ ）为。

查看试题解析
15. 如图，平面内有16个格点，每个格点小正方形的边长为1，则图中阴影部分的面积为．

查看试题解析
16. 若抛物线 $y_{1} = a_{1} x^{2} + b_{1} x + c_{1}$ 与 $y_{2} = a_{2} x^{2} + b_{2} x + c_{2}$ 满足 $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}} = k (k \neq 0 ， 1)$ ，则称 $y_{1} ， y_{2}$ 互为“相关抛物线”给出如下结论：
①y₁与y₂的开口方向，开口大小不一定相同； ②y₁与y₂的对称轴相同；③若y₂的最值为m，则y₁的最值为k²m；④若函数 $y_{2} = a_{2} x^{2} + b_{2} x + c_{2}$ 与x 轴的两交点间距离为d，则函数 $y_{1} = a_{1} x^{2} + b_{1} x + c_{1}$ 与x 轴的两交点间距离也为 $d$ .其中正确的结论的序号是（把所有正确结论的序号都填在横线上）.

查看试题解析

三、解答题

17. 先化简，再求值： $\frac{x + 2}{x} - \frac{x + 4}{x + 2}$ ，其中 $x^{2} + 2 x - 15 = 0$

查看试题解析
18. 把大小和形状完全相同的6张卡片分成两组，每组3张，分别标上1、2、3，将这两组卡片分别放入两个盒子中搅匀，再从中随机抽取一张．

(1)、试求取出的两张卡片数字之和为奇数的概率；

(2)、若取出的两张卡片数字之和为奇数，则甲胜；取出的两张卡片数字之和为偶数，则乙胜；试分析这个游戏是否公平？请说明理由．

查看试题解析
19. 在学完《二次函数》后，老师给小明布置了家庭作业：
小明已正确地完成作业（上图中抛物线y₂的图象的对称轴为直线x=-1），由于不小心表格中的y₂的解析式和部分数据被污渍覆盖了，请你根据作业单上的信息求出a，b，y₂的解析式.

查看试题解析
20. 如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A（0，2），B（4，2）C（6，0），解答下列问题：

(1)、请在图中确定该圆弧所在圆心D点的位置，则D点坐标为；

(2)、连结AD，CD，求⊙D的半径（结果保留根号）；

(3)、求扇形DAC的面积. （结果保留π）

查看试题解析
21. 如图，圆O的直径为5，在圆O上位于直径AB的异侧有定点C和动点P，已知BC：CA=4： 3，点P在半圆弧AB上运动（不与A、B两点重合），过点C作CP的垂线CD交PB的延长线于D点．

(1)、求证：AC·CD=PC·BC；

(2)、当点P运动到AB弧中点时，求CD的长；

(3)、当点P运动到什么位置时，△PCD的面积最大？并求出这个最大面积S。

查看试题解析
22. 现有一生产季节性产品的企业，有两种营销方案，经测算：方案一，一年中获得的每月利润y（万元）和月份x的关系为 $y = - 0.5 x^{2} + 8 x - 14$ ；方案二，一年中获得的每月利润y（万元）与月份x的关系为 $y = - x^{2} + 14 x - 24$ ．两个函数部分图象如图所示：

(1)、请你指出：方案一，月利润对应的图象是；方案二，月利润对应的图象是；（填序号）

(2)、该企业一年中月利润最高可达万元；

(3)、生产季节性产品的企业，当它的产品无利润时就会立即停产，企业原计划全年使用营销方案二进行销售，
则①该企业一年中应停产的月份是几月？
②为了使全年能获得更高利润，企业应该如何改进其营销方案，使全年总利润最高？并算出全年最高总利润比原计划多多少？

查看试题解析
23. 已知二次函数y=（t-4）x²-（2t-5）x+4在x=0与x=5的函数值相等．

(1)、求二次函数的解析式；

(2)、若二次函数的图象与x轴交于A，B两点（A在B左侧），与y轴交于点C，一次函数y=kx+b经过B，C两点，求一次函数的表达式；

(3)、在（2）的条件下，过动点D（0，m）作直线 $l$ //x轴，其中．将二次函数图象在直线 $l$ 下方的部分沿直线 $l$ 向上翻折，其余部分保持不变，得到一个新图象M．若直线 $y = k x + b$ 与新图象M恰有两个公共点，请求出 $m$ 的取值范围．

查看试题解析