黑龙江省哈尔滨六十九中2017届九年级上学期数学月考试卷

试卷更新日期：2018-09-26 类型：月考试卷

进入出卷网下载

一、单选题

1. ﹣ $\frac{1}{3}$ 的倒数是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 地球上的陆地面积约为149000000km² ．将149000000用科学记数法表示为（）

A、1.49×10⁶ B、1.49×10⁷ C、1.49×10⁸ D、1.49×10⁹

查看试题解析
3. 下列运算中，计算结果正确的是（）

A、a²×a³=a⁶ B、2a+3b=5ab C、a⁵÷a²=a³ D、（a²b）²=a⁴b

查看试题解析
4. 下面的图案中，是轴对称图形而不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，矩形AOBC的面积为4，反比例函数 $y = \frac{k}{x}$ 的图象的一支经过矩形对角线的交点P，则该反比例函数的解析式是（）

A、 $y = \frac{4}{x}$ B、 $y = \frac{2}{x}$ C、 $y = \frac{1}{x}$ D、 $y = \frac{1}{2 x}$

查看试题解析
6. 反比例函数 $y = \frac{2 k}{x}$ 的图象经过点（﹣2，3），则k的值为（）

A、3 B、﹣ $\frac{7}{2}$ C、 $\frac{7}{2}$ D、﹣3

查看试题解析
7. 如图，在长方形ABCD中，AB=3，BC=4，若沿折痕EF折叠，使点C与点A重合，则折痕EF的长为（）

A、 $\frac{15}{8}$ B、 $\frac{15}{4}$ C、 $\frac{15}{2}$ D、15

查看试题解析
8. 如图，将△ABC绕点C顺时针方向旋转40°，得△A′B′C，若AC⊥A′B′，则∠A等于（）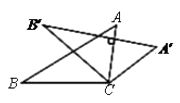

A、50° B、60° C、70° D、80°

查看试题解析
9. 在菱形ABCD中，若∠ADC=120°，则BD：AC等于（）

A、 $\sqrt{3}$ ：2 B、 $\sqrt{3}$ ：3 C、1：2 D、 $\sqrt{3}$ ：1

查看试题解析
10. 小聪和小明分别从相距30公里的甲、乙两地同时出发相向而行，小聪骑摩托车到达乙地后立即返回甲地，小明骑自行车从乙地直接到达甲地，函数图象y₁（km）和y₂（km）分别表示小聪离甲地的距离和小明离乙地的距离与已用时间t（h）之间的关系，如图所示．下列说法：①折线段OAB是表示小聪的函数图象y₁ ，线段OC是表示小明的函数图象y₂；②小聪去乙地和返回甲地的平均速度相同；③两人在出发80分钟后第一次相遇；④小明骑自行车的平均速度为15km/h，其中不正确的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

11. 化简 $\sqrt{8}$ ＋ $\sqrt{\frac{1}{8}}$ ＝.

查看试题解析
12. 函数 $y = \frac{2}{x + 1}$ 中，自变量x的取值范围是．

查看试题解析
13. 分解因式：a²﹣ab= ．

查看试题解析
14. 一元二次方程x²=2x的根是．

查看试题解析
15. 反比例函数 $y = - \frac{2}{x}$ ，当x＞0时，y的取值范围是．

查看试题解析
16. 如图，△ABC是等腰直角三角形，BC是斜边，现将△ABP绕点A逆时针旋转后能与△ACP′重合，已知AP=4，则PP′长度为．

查看试题解析
17. 反比例函数 $y = \frac{k}{x}$ （k≠0）的图象经过点（2，5），若点（1，n）在反比例函数的图象上，则n的值是．

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，按图中所示方法将△BCD沿BD折叠，使点C落在边AB上的点C′处，则折痕BD的长为．

查看试题解析
19. 已知正方形ABCD边长为4，在直线DC上有一点E，且DE=1，过点A作AE的垂线交直线BC于点F，则CF的长为．

查看试题解析
20. 在△ABC中，AB=AC，∠BAC=90°，点E在AC边上，BE平分∠ABC，CD⊥BE于点D，连接AD，若BE=10，则AD的长是．

查看试题解析

三、解答题

21. 先化简，再求代数式 $\frac{m^{2} - 2 m + 1}{m^{2} - 1}$ ÷（m﹣1）的值，其中m= $\sqrt{3}$ ﹣1．

查看试题解析
22. 如图，在平面直角坐标系中，点O是坐标原点，B、C两点的坐标分别为（3，﹣1），（2，1）．

(1)、以O点为中心在y轴的左侧作出△OBC中心对称图形△OB′C′，其中点C与C′是对应点，画出图形；

(2)、直接写出C′点的坐标为；

(3)、△OBC的面积为 $\frac{5}{2}$ ，直接写出△OB′C′的面积为．

查看试题解析
23. 如图所示，若△ABC、△ADE都是正三角形，请试比较：线段BD与线段CE的大小？写出你的猜想，并说明理由．

查看试题解析
24. 一艘轮船以每小时20海里的速度沿正北方向航行，在A处测得灯塔C在北偏西30°方向上，轮船航行2小时后，到达B处，在B处测得灯塔C北偏西60°方向上，当轮船到达灯塔C的正东方向的D处时，如图所示，求轮船与灯塔C的距离（结果保留根号）？

查看试题解析
25. 如图，在平面直角坐标系中，点O为坐标原点，正方形OABC的边OA，OC分别在x轴，y轴上，点B的坐标为(2，2)，反比例函数y＝ $\frac{k}{x}$ (x＞0，k≠0)的图象经过线段BC的中点D．

(1)、求k的值；

(2)、若点P(x，y)在该反比例函数的图象上运动(不与点D重合)，过点P作PR⊥y轴于点R，作PQ⊥BC所在直线于点Q，记四边形CQPR的面积为S，求S关于x的函数解析式并写出x的取值范围．

查看试题解析
26. 某学校计划组织师生参加哈尔滨冰雪节，感受冰雪艺术的魅力．出租公司现有甲、乙两种型号的客车可供租用，且每辆乙型客车的租金比每辆甲型客车少60元．若该校租用3辆甲种客车，4辆乙种客车，则需付租金1720元．

(1)、该出租公司每辆甲、乙两型客车的租金各为多少元？

(2)、若学校计划租用6辆客车，租车的总租金不超过1560元，那么最多租用甲型客车多少辆？

查看试题解析
27. 已知：如图直线y= $\frac{1}{3}$ x+2与抛物线y=ax²交于A．B两点，点B的坐标（3，m），直线AB交y轴于点C．

(1)、求a，m的值；

(2)、点P在对称轴右侧的抛物线上，设P点横坐标为t，△PAB的面积为s，求s与t的函数关系式；

(3)、在（2）的条件下，在x轴上有一点Q，当以B．C．P．Q为顶点的四边形是平行四边形时，求点Q的坐标．

查看试题解析