黑龙江省大庆市肇源县2017届九年级上学期数学10月月考试卷
试卷更新日期:2018-09-26 类型:月考试卷
一、单选题
-
1. 不等式-3x≥6的解集在数轴上表示为( )A、
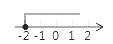 B、
B、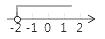 C、
C、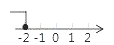 D、
D、 2. 已知等腰三角形一腰上的高线与另一腰的夹角为50°,那么这个等腰三角形的顶角等于( )A、15°或75° B、140° C、40° D、140°或40°3. 已知AB=6cm,P是到A,B两点距离相等的点,则AP的长为( )A、3cm B、4cm C、5cm D、不能确定4. 如图,直线 l1 , l2 , l3、 表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )
2. 已知等腰三角形一腰上的高线与另一腰的夹角为50°,那么这个等腰三角形的顶角等于( )A、15°或75° B、140° C、40° D、140°或40°3. 已知AB=6cm,P是到A,B两点距离相等的点,则AP的长为( )A、3cm B、4cm C、5cm D、不能确定4. 如图,直线 l1 , l2 , l3、 表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )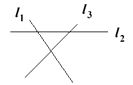 A、一处 B、二处 C、三处 D、四处5. 在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,则AB边上的中线长为( )A、1 B、2 C、1.5 D、6. 如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,若△DEC的周长是10cm,则BC=( )
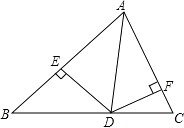
A、一处 B、二处 C、三处 D、四处5. 在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,则AB边上的中线长为( )A、1 B、2 C、1.5 D、6. 如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,若△DEC的周长是10cm,则BC=( )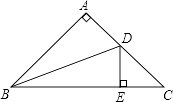 A、8cm B、10cm C、11cm D、12cm7. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED②AC+BE=AB ③∠BDE=∠BAC ④AD平分∠CDE ⑤S△ABD∶S△ACD=AB∶AC,其中正确的有( )
A、8cm B、10cm C、11cm D、12cm7. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED②AC+BE=AB ③∠BDE=∠BAC ④AD平分∠CDE ⑤S△ABD∶S△ACD=AB∶AC,其中正确的有( )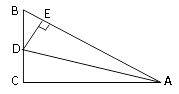 A、2个 B、3个 C、4个 D、5个8. 不等式 去分母后正确的是( )A、 B、 C、 D、9. 已知不等式4x-a≤0的正整数解是1,2,则a的取值范围是( )A、8<a<12 B、8≤a<12 C、8<a≤12 D、8≤a≤12
A、2个 B、3个 C、4个 D、5个8. 不等式 去分母后正确的是( )A、 B、 C、 D、9. 已知不等式4x-a≤0的正整数解是1,2,则a的取值范围是( )A、8<a<12 B、8≤a<12 C、8<a≤12 D、8≤a≤12二、填空题
-
10. 不等式 的正整数解是 .11. 若a>b,且c为有理数,则ac2 bc2 .12. 当x时,代数式 的值是正数.13. 若不等式ax|a-1|>2是一元一次不等式,则a= .14. 一种药品的说明书上写着:“每日用量60~120mg,分4次服用”,一次服用这种药量x(mg)范围为 mg.
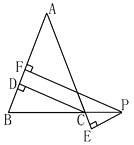
15. 如果一个等腰三角形的一个角等于80°,则底角的度数是 .16. 如图,在△ABC中,∠C=90°,AD是角平分线,AC=5,DC=3,则点D到AB的距离是 .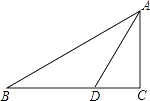 17. 在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,且∠ADC=100°,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 .
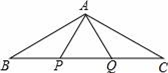
17. 在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,且∠ADC=100°,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 .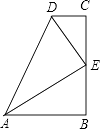 18. △ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为500 , 则∠B=19. 在Rt△ABC中,∠C=90°,∠A=30°,若要在直线BC或直线AC上取一点P,使△ABP是等腰三角形,符合条件的点P有个点.20. 铁路部门规定旅客免费携带行李箱的长宽高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽之比为3:2,则该行李箱长度的最大值是cm.
18. △ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为500 , 则∠B=19. 在Rt△ABC中,∠C=90°,∠A=30°,若要在直线BC或直线AC上取一点P,使△ABP是等腰三角形,符合条件的点P有个点.20. 铁路部门规定旅客免费携带行李箱的长宽高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽之比为3:2,则该行李箱长度的最大值是cm.
三、解答题
-
21. 解不等式x-2(x-1)>0,并将它的解集在数轴上表示出来.
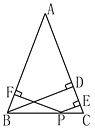
 22. 如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.
22. 如图,在等边三角形ABC中,BD⊥AC于D,延长BC到E,使CE=CD,AB=6cm.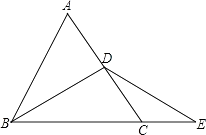 (1)、求BE的长;
(1)、求BE的长;
(2)、判断△BDE的形状,并说明理由.23. B,C,D三点在一条直线上,△ABC和△ECD是等边三角形.求证:BE=AD.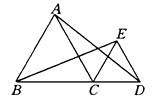 24. 解答下列各题:
24. 解答下列各题:
(1)、x取何值时,代数式3x+2的值不大于代数式4x+3的值?
(2)、当m为何值时,关于x的方程 x-1=m的解不小于3?
(3)、已知不等式2(x+3)-4<0, 化简:︳4x+1︱-︱2-4x︱.25. △ABC中,AD为角平分线,DE⊥AB于E,DF⊥AC于F,AB=10cm,AC=8cm,△ABC的面积为54cm2 , 求DE的长.