上海市闵行区2016-2017学年八年级下学期数学期末考试试卷
试卷更新日期：2018-09-26 类型：期末考试
一、单选题
-
1. 一次函数y=2﹣x的图象与y轴的交点坐标为（ ）A、（2，0） B、（0，2） C、（﹣2，0） D、（0，﹣2）2. 下列方程中，有实数根的是（ ）A、 =0 B、 + =0 C、 =2 D、 + =23. 下列命题中的假命题是（ ）A、一组邻边相等的平行四边形是菱形 B、一组邻边相等的矩形是正方形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边相等且有一个角是直角的四边形是矩形4. 如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（ ）
A、
B、
C、
D、
5. 闵行体育公园内有一个形状是平行四边形的花坛（如图），并且AB∥EF∥DC，BC∥GH∥AD，花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花．如果小杰不小心把球掉入花坛，那么下列说法中错误的是（ ）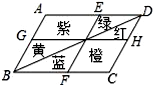
A、球落在红花丛中和绿花丛中的概率相等 B、球落在紫花丛中和橙花丛中的概率相等 C、球落在红花丛中和蓝花丛中的概率相等 D、球落在蓝花丛中和黄花丛中的概率相等6. 如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，联结EF、CF，那么下列结论中一定成立的个数是（ ）①∠DCF= ∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 函数y=﹣ x+1的图象不经过第象限．8. 已知直线y=（k+2）x+ 的截距为1，那么该直线与x轴的交点坐标为9. 在函数y=﹣3x+7中，如果自变量x大于2，那么函数值y的取值范围是 ．10. 已知一次函数y= x+m﹣1（其中m是常数），如果函数值y随x的增大而减小，且与y轴交于点P（0，t），那么t的取值范围是 ．11. 方程3x3﹣2x=0的实数解是 ．12. 方程2 =x﹣6的根是 ．13. 化简： + ﹣ = ．14. 布袋内装有大小、形状相同的3个红球和1个白球，从布袋中一次摸出两个球，那么两个都摸到红球的概率是 ．15. 某件商品连续两次降价后，零售价为原来的64%，那么此商品平均每次降价的百分率为 ．16. 一个多边形的内角和是1440°，那么这个多边形边数是 ．17. 如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，四边形ABCD还应满足的一个条件是 ．
18. 如图，现有一张矩形纸片ABCD，其中AB=4cm，BC=6cm，点E是BC的中点．将纸片沿直线AE折叠，使点B落在梯形AECD内，记为点B′，那么B′、C两点之间的距离是 cm．
三、解答题
-
19. 解关于x的方程：bx2﹣1=1﹣x2（b≠﹣1）．20. 解方程：x2+2x﹣ =1．21. 解方程组： ．22. 如图，已知点E在四边形ABCD的边AB上，设 ， ，
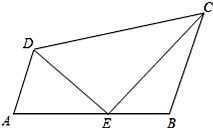(1)、试用向量 、 和 表示向量 ， ；(2)、在图中求作： （不要求写出作法，只需写出结论即可）23. 已知把直线y=kx+b（k≠0）沿着y轴向上平移3个单位后，得到直线y=﹣2x+5．
(1)、求直线y=kx+b（k≠0）的解析式；(2)、求直线y=kx+b（k≠0）与坐标轴围成的三角形的周长．24. 已知：如图，等腰梯形ABCD的中位线EF的长为6cm，对角线BD平分∠ADC，下底BC的长比等腰梯形的周长小20cm，求上底AD的长．
25. 闵行区政府为残疾人办实事，在道路改造工程中为盲人修建一条长3000米的盲道，根据规划设计和要求，某工程队在实际施工中增加了施工人员，每天修建的盲道比原计划多250米，结果提前2天完成工程，问实际每天修建盲道多少米．
26. 如图1，已知△OAB、△OBC、△OCD、△ODE、△OEF和△OFA均为边长为a的等边三角形，点P为边BC上任意一点，过P作PM∥AB交AF于M，作PN∥CD交DE于N．
(1)、那么∠MPN= ， 并求证PM+PN=3a；(2)、如图2，联结OM、ON．求证：OM=ON；(3)、如图3，OG平分∠MON，判断四边形OMGN是否为特殊四边形，并说明理由．