新人教版数学八年级上册第十三章轴对称13.1.2线段的垂直平分线的性质同步练习
试卷更新日期：2015-08-14 类型：同步测试
一、选择题
-
1. 如图，在△ABC中，分别以点A和点B为圆心，大于线段AB的长为半径画孤，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，若△ADC的周长为10，AB＝7，则△ABC的周长为（ ）
A、7 B、14 C、17 D、202. 如下图，在
中，∠C＝90°，BE平分∠ABC，ED垂直平分AB于D．若AC＝9，则AE的值是（ ） 
A、2 B、4 C、6 D、83. 如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝5，则线段PB的长度为（ ）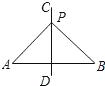
A、6 B、5 C、4 D、34. 如图，等腰△ABC中，AB＝AC，∠A＝20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）
A、80° B、60° C、40° D、20°5. 如图，直线CP是AB的中垂线且交AB于P，其中AP＝2CP．甲、乙两人想在AB上取两点D、E，使得AD＝DC＝CE＝EB，其作法如下：甲：作∠ACP、∠BCP之角平分线，分别交AB于D、E，则D、E即为所求；
乙：作AC、BC之中垂线，分别交AB于D、E，则D、E即为所求．
对于甲、乙两人的作法，下列判断何者正确（ ）
A、两人都正确 B、两人都错误 C、甲正确，乙错误 D、甲错误，乙正确6. 如图，在
中，∠C＝90°，∠B＝30°．AB的垂直平分线DE交AB于点D，交BC于点E，则下列结论不正确的是（ ） 
A、AE＝BE B、AC＝BE C、CE＝DE D、∠CAE＝∠B7. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（ ）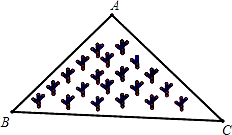
A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点8. 如图，AC＝AD，BC＝BD，则有（ ）
A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB9. 如图，在△ABC中，∠B＝30°，ED垂直平分BC，ED＝3．则CE长为（ ）
A、6 B、9 C、3 D、810. 如图，△ABC中，DE垂直平分AC交AB于E，∠A＝30°，∠ACB＝80°，则∠BCE的度数为（ ）
A、80° B、70° C、60° D、50°11. 如图，等腰三角形ABC中，已知AB＝AC，∠A＝30°，AB的垂直平分线交AC于D，则∠CBD的度数为（ ）
A、50° B、30° C、75° D、45°12. 如图，在△ABC中，BC边上的垂直平分线DE与边BC交于点D，边AB交于点E．若△EDC的周长为24，△ABC与四边形AEDC的周长之差为12，则线段DE的长为（ ）
A、12 B、6 C、24 D、3613. 已知A和B两点在线段EF的中垂线上，且∠EBF＝100°，∠EAF＝70°，则∠AEB等于( )A、95° B、15° C、95°或15° D、170°或30°14. 如图，AB＝AC，∠BAC＝120°，AB的垂直平分线交BC于点D，那么∠ADC的度数为（ ）
A、120° B、30° C、60° D、80°15. 如图，∠ABC＝50°，AD垂直且平分BC于点D，∠ABC的平分线BE交AD于点E，连接EC，则∠AEC的度数是（ ）
A、50° B、25° C、80° D、115°二、填空题
-
16.
如图，有一腰长为5cm，底边长为4cm的等腰三角形纸片，沿着底边上的中线将纸片剪开，得到两个全等的直角三角形纸片，用这两个直角三角形纸片拼成的平面图形中有个不同的四边形．
17.已知如图，在△ABC中，BC＝8，AB的中垂线交BC于D，AC的中垂线交BC与E，则△ADE的周长等于 ．
18.如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，且AB＝AC，AC＝AD，有如下四个结论：①AC⊥BD；②BC＝DE；③∠DBC＝∠DAC；④△ABC是正三角形．请写出正确结论的序号（把你认为正确结论的序号都填上）
19.如图，△ABC的周长为19cm，AC的垂直平分线DE交BC于D，E为垂足，AE＝3cm，则△ABD的周长为cm．
20. 在△ABC中，∠A＝50°，AB＝AC，AB的垂直平分线DE交AC于D，则∠DBC的度数是°．三、解答题
-
21.
如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC．
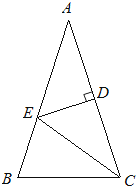(1)、求∠ECD的度数；(2)、若CE＝5，求BC长．22.如图，在直角△ABC中，∠C＝90°，∠CAB的平分线AD交BC于D，若DE垂直平分AB，求∠B的度数．
23.如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F．
求证：
(1)、FC＝AD
(2)、AB＝BC＋AD．
