滨海新区七所重点学校2018届高三毕业班理数联考数学试卷

试卷更新日期：2018-09-21 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数 $z$ 满足 $(1 - i) z = - 3 + i$ ，则 $z$ 在平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 若实数 $x$ ， $y$ 满足 ${\begin{matrix} x + y - 1 \leq 0 \\ x - y \leq 0 \\ x \geq 0 \end{matrix}$ ，则 $z = 2 x - 3 y$ 的最小值是（）

A、 $1$ B、 $- \frac{1}{2}$ C、 $- 3$ D、 $0$

查看试题解析
3. 某程序框图如图所示，该程序运行后输出的k的值是（）

A、4 B、5 C、6 D、7

查看试题解析
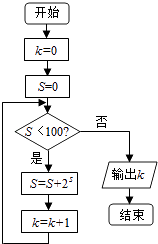4. 已知集合 $A = {x | | x - 1 | + | x - 4 | < 5}$ ，集合 $B = {x | | y = {log}_{2} (2 x - x^{2})}$ ，则“ $x \in A$ ”是“ $x \in B$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 若 $a = \ln 2$ ， $b = 5^{- \frac{1}{2}}$ ， $c = \frac{1}{4} \int_{0}^{π} \sin x d x$ ，则 $a ， b ， c$ 的大小关系（）

A、 $a < b < c$ B、 $b < a < c$ C、 $c < b < a$ D、 $b < c < a$

查看试题解析
6. 在 $△ A B C$ 中， $sin (B - C) + sin A = \frac{3}{2}$ ， $A C = \sqrt{3} A B$ ，则角 $C =$ （）

A、 $\frac{π}{2}$ B、 $\frac{π}{3}$ C、 $\frac{π}{6}$ 或 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析
7. 已知双曲线 $\frac{x^{2}}{3} - y^{2} = 1$ 的右焦点恰好是抛物线 $y^{2} = 2 p x$ （ $p > 0$ ）的焦点 $F$ ，且 $M$ 为抛物线的准线与 $x$ 轴的交点， $N$ 为抛物线上的一点，且满足 $| N F | = \frac{\sqrt{3}}{2} | M N |$ ，则点 $F$ 到直线 $M N$ 的距离为（）

A、 $\frac{1}{2}$ B、 $1$ C、 $\sqrt{3}$ D、 $2$

查看试题解析
8. 已知函数 $f (x) = {\begin{matrix} \frac{x}{e^{x}} + 1 (x \geq 0) \\ x^{2} + 2 x + 1 (x < 0) \end{matrix}$ ，若函数 $y = f (f (x) - a) - 1$ 有三个零点，则实数 $a$ 的取值范围是（）

A、 $(1 ， 1 + \frac{1}{e}) \cup (2 ， 3]$ B、 $(1 ， 1 + \frac{1}{e}) \cup (2 ， 3] \cup {3 + \frac{1}{e}}$ C、 $(1 ， 1 + \frac{1}{e}) \cup [2 ， 3) \cup {3 + \frac{1}{e}}$ D、 $(1 ， 1 + \frac{2}{e}) \cup (2 ， 3]$

查看试题解析

二、填空题

9. 在二项式 ${(x^{2} - \frac{1}{x})}^{5}$ 的展开式中，含 $x^{7}$ 的项的系数是

查看试题解析
10. 已知曲线 $C$ 的极坐标方程是 $ρ = 4 cos θ$ .以极点为平面直角坐标系的原点，极轴为 $x$ 轴的非负半轴，建立平面直角坐标系，直线 $l$ 的参数方程是 ${\begin{matrix} x = 1 + \frac{\sqrt{2}}{2} t \\ y = \frac{\sqrt{2}}{2} t \end{matrix}$ （ $t$ 为参数），若直线 $l$ 与曲线 $C$ 相交于 $A$ ， $B$ 两点，则 $| A B | =$

查看试题解析
11. 某几何体的三视图如图所示，俯视图是由一个半圆与其直径组成的图形，则此几何体的体积是

查看试题解析
12. 在平行四边形 $A B C D$ 中， $A B = 2$ ， $A D = 1$ ， $∠ B A D = 60 °$ ， $E$ 为 $C D$ 的中点，若 $F$ 是线段 $B C$ 上一动点，则 $\overset{⇀}{A F} \cdot \overset{⇀}{F E}$ 的取值范围是

查看试题解析
13. 若正实数 $x$ ， $y$ ，满足 $x + 2 y = 5$ ，则 $\frac{x^{2} - 3}{x + 1} + \frac{2 y^{2} - 1}{y}$ 的最大值是．

查看试题解析
14. $3$ 个男生和 $3$ 个女生排成一列，若男生甲与另外两个男同学都不相邻，则不同的排法共有种（用数字作答）．

查看试题解析

三、解答题

15. 已知函数 $f (x) = \sqrt{3} cos x cos (x - \frac{π}{2}) + {sin}^{2} (x - \frac{π}{6}) - \frac{1}{2}$ .

(1)、求 $f (x)$ 的单调递增区间；

(2)、若 $x \in [0 ， \frac{π}{4}]$ ， $f (x) = \frac{\sqrt{3}}{6}$ ，求 $cos 2 x$ 的值.

查看试题解析
16. 某单位年会进行抽奖活动，在抽奖箱里装有 $1$ 张印有“一等奖”的卡片， $2$ 张印
有“二等奖”的卡片， 3张印有“新年快乐”的卡片，抽中“一等奖”获奖 $200$ 元，抽中“二等奖”获奖 $100$ 元，抽中“新年快乐”无奖金.

(1)、单位员工小张参加抽奖活动，每次随机抽取一张卡片，抽取后不放回.假如小张一定要将所有获奖卡片全部抽完才停止. 记 $A$ 表示“小张恰好抽奖 $4$ 次停止活动”，求 $P (A)$ 的值；

(2)、若单位员工小王参加抽奖活动，一次随机抽取 $2$ 张卡片.
① $% 2$ 记 $B$ 表示“小王参加抽奖活动中奖”，求 $P (B)$ 的值；
②设 $X$ 表示“小王参加抽奖活动所获奖金数（单位：元）”，求 $X$ 的分布列和数学期望.

查看试题解析
17. 在四棱锥 $P - A B C D$ 中， $P D ⊥$ 平面 $A B C D$ ， $A B ∥ D C$ ， $A B ⊥ A D$ ， $D C = A D = 1$ ， $A B = 2$ ， $∠ P A D = 45 °$ ， $E$ 是 $P A$ 的中点， $F$ 在线段 $A B$ 上，且满足 $\overset{⇀}{C F} \cdot \overset{⇀}{B D} = 0$ .

(1)、求证： $D E ∥$ 平面 $P B C$ ；

(2)、求二面角 $F - P C - B$ 的余弦值；

(3)、在线段 $P A$ 上是否存在点 $Q$ ，使得 $F Q$ 与平面 $P F C$ 所成角的余弦值是 $\frac{\sqrt{6}}{3}$ ，若存在，求出 $A Q$ 的长；若不存在，请说明理由.

查看试题解析
18. 已知数列 ${a_{n}}$ 的前 $n$ 项和是 $S_{n}$ ，且 $S_{n} + \frac{1}{2} a_{n} = 1 (n \in N^{*})$ .数列 ${b_{n}}$ 是公差 $d$ 不等于 $0$ 的等差数列，且满足： $b_{1} = \frac{3}{2} a_{1}$ ， $b_{2}$ ， $b_{5}$ ， $b_{14}$ 成等比数列.

(1)、求数列 ${a_{n}}$ 、 ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = a_{n} \cdot b_{n}$ ，求数列 ${c_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
19. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为 $F_{2} (3 ， 0)$ ，离心率为 $e$ .

(1)、若 $e = \frac{\sqrt{3}}{2}$ ，求椭圆的方程；

(2)、设直线 $y = k x$ 与椭圆相交于 $A ， B$ 两点， $M ， N$ 分别为线段 $A F_{2} ， B F_{2}$ 的中点，若坐标原点 $O$ 在以 $M N$ 为直径的圆上，且 $\frac{\sqrt{2}}{2} < e \leq \frac{\sqrt{3}}{2}$ ，求 $k$ 的取值范围.

查看试题解析
20. 已知函数 $f (x) = ln x$ ， $g (x) = \frac{1}{2} a x^{2} + b x$ ， $a \neq 0$

(1)、若 $a = 1$ ，且 $h (x) = f (x) + g (x)$ 在其定义域上存在单调递减区间，求实数 $b$ 的取值范围；

(2)、设函数 $φ (x) = x f (x) + (m - x) f (m - x)$ ， $0 < x < m$ ，若 $φ (x) \geq 2 m - m^{2}$ 恒成立，求实数 $m$ 的取值范围；

(3)、设函数 $f (x)$ 的图象 $C_{1}$ 与函数 $g (x)$ 的图象 $C_{2}$ 交于点 $P$ 、 $Q$ ，过线段 $P Q$ 的中点作 $x$ 轴的垂线分别交 $C_{1}$ ， $C_{2}$ 于点 $M$ 、 $N$ ，证明： $C_{1}$ 在点 $M$ 处的切线与 $C_{2}$ 在点 $N$ 处的切线不平行.

查看试题解析