2018-2019学年数学人教版（五四学制）九年级上册28.1.3二次函数y=ax²+bx+c的图像性质同步课时作业(2)

试卷更新日期：2018-09-18 类型：同步测试

进入出卷网下载

一、选择题

1. 把二次函数y=x²﹣4x+1化成y=a（x+m）²+k的形式是（　　）

A、y=（x﹣2）²+1 B、y=（x﹣2）²﹣1 C、y=（x﹣2）²+3 D、y=（x﹣2）²﹣3

查看试题解析
2. 已知二次函数y＝－3x²＋1的图象如图所示，将其沿x轴翻折后得到的抛物线的表达式为( )

A、y＝－3x²－1 B、y＝3x² C、y＝3x²＋1 D、y＝3x²－1

查看试题解析
3. 把抛物线 $y = {(x + 1)}^{2}$ 向下平移2个单位，再向右平移1个单位，所得到的抛物线是（）

A、 $y = {(x + 2)}^{2} + 2$ B、 $y = {(x + 2)}^{2} - 2$ C、 $y = x^{2} + 2$ D、 $y = x^{2} - 2$

查看试题解析
4. 二次函数的图象经过 $(0 ， 3) (- 2 ， - 5) (1 ， 4)$ 三点，则它的解析式为（）

A、 $y = x^{2} + 6 x + 3$ B、 $y = - 3 x^{2} - 2 x + 3$ C、 $y = 2 x^{2} + 8 x + 3$ D、 $y = - x^{2} + 2 x + 3$

查看试题解析
5. 二次函数的图象如图所示，则这个二次函数的解析式为（）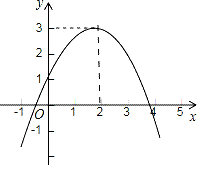

A、y= $\frac{1}{2}$ （x﹣2）²+3 B、y= $\frac{1}{2}$ （x﹣2）²﹣3 C、y=﹣ $\frac{1}{2}$ （x﹣2）²+3 D、y=﹣ $\frac{1}{2}$ （x﹣2）²﹣3

查看试题解析
6. 将二次函数y=x²的图象先向下平移1个单位，再向右平移3个单位，得到的图象与一次函数y=2x+b的图象有公共点，则实数b的取值范围是（）

A、b＞8 B、b＞﹣8 C、b≥8 D、b≥﹣8

查看试题解析
7. 对称轴平行于y轴的抛物线的顶点为点（2，3）且抛物线经过点（3，1），那么抛物线解析式是（）

A、y=﹣2x²+8x+3 B、y=﹣2x^‑2﹣8x+3 C、y=﹣2x²+8x﹣5 D、y=﹣2x^‑2﹣8x+2

查看试题解析
8. 若二次函数 $y = a x^{2} + b x + c (a < 0)$ 的图象经过点（2，0），且其对称轴为 $x = - 1$ ，则使函数值 $y > 0$ 成立的 $x$ 的取值范围是（）

A、 $x < - 4$ 或 $x > 2$ B、 $- 4$ ≤ $x$ ≤ $2$ C、 $x$ ≤ $- 4$ 或 $x$ ≥ $2$ D、 $- 4 < x < 2$

查看试题解析

二、填空题

9. 与抛物线 $y = x^{2} - 2 x + 3$ 关于 $x$ 轴对称的抛物线解析式是．

查看试题解析
10. 一抛物线和抛物线y=﹣2x²的形状、开口方向完全相同，顶点坐标是（﹣1，3），则该抛物线的解析式为．

查看试题解析
11. 抛物线y=ax²+bx+c中，已知a：b：c=1：2：3，y最小值为6，则此抛物线的解析式为．

查看试题解析
12. 请写出一个图象的对称轴为y轴，开口向下，且经过点（1，﹣2）的二次函数解析式，这个二次函数的解析式可以是．

查看试题解析
13. 如图4所示的是桥梁的两条钢缆具有相同的抛物线形状．按照图中建立的直角坐标系，右面的一条抛物线的解析式为y=x²－4x+5表示，而且左右两条抛物线关于y轴对称，则左面钢缆的表达式为．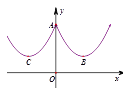

查看试题解析
14. 邓老师设计了一个计算程序，输入和输出的数据如下表：
入数据
1
2
3
4
5
6
…
输出数据
$\frac{1}{2}$
$\frac{2}{7}$
$\frac{3}{14}$
$\frac{4}{23}$
$\frac{5}{34}$
$\frac{6}{47}$
…
那么，当输入数据是7时，输出的数据是．

查看试题解析

三、解答题

15. 已知抛物线y＝ax²＋x＋2经过点(－1，0)．

(1)、求a的值，并写出这条抛物线的顶点坐标．

(2)、若点P(t，t)在抛物线上，则点P叫做抛物线上的不动点，求出这个抛物线上所有不动点的坐标．

查看试题解析
16. 已知抛物线y=x²﹣4x+3．

(1)、用配方法将y=x²﹣4x+3化成y=a（x﹣h）²+k的形式；

(2)、求出该抛物线的对称轴和顶点坐标；

(3)、直接写出当x满足什么条件时，函数y＜0．

查看试题解析
17. 如图，已知点A（0，2），B（2，2），C（﹣1，﹣2），抛物线F：y=x²﹣2mx+m²﹣2与直线x=﹣2交于点P．

(1)、当抛物线F经过点C时，求它的表达式；

(2)、设点P的纵坐标为y_P ，求y_P的最小值，此时抛物线F上有两点（x₁ ， y₁），（x₂ ， y₂），且x₁＜x₂≤﹣2，比较y₁与y₂的大小；

(3)、当抛物线F与线段AB有公共点时，直接写出m的取值范围．

查看试题解析
18. 在平面直角坐标系xOy中，过点（0，2）且平行于x轴的直线，与直线y=x﹣1交于点A，点A关于直线x=1的对称点为B，抛物线C₁：y=x²+bx+c经过点A，B．

(1)、求点A，B的坐标；

(2)、求抛物线C₁的表达式及顶点坐标；

(3)、若抛物线C₂：y=ax²（a≠0）与线段AB恰有一个公共点，结合函数的图象，求a的取值范围．

查看试题解析
19. 在平面直角坐标系中，二次函数y=x²+mx+2m﹣7的图象经过点（1，0）．

(1)、求抛物线的表达式；

(2)、把﹣4＜x＜1时的函数图象记为H，求此时函数y的取值范围；

(3)、在（2）的条件下，将图象H在x轴下方的部分沿x轴翻折，图象H的其余部分保持不变，得到一个新图象M．若直线y=x+b与图象M有三个公共点，求b的取值范围．

查看试题解析

入数据	1	2	3	4	5	6	…
输出数据	$\frac{1}{2}$	$\frac{2}{7}$	$\frac{3}{14}$	$\frac{4}{23}$	$\frac{5}{34}$	$\frac{6}{47}$	…