2018-2019学年数学人教版（五四学制）九年级上册28.1.3二次函数y=a(x-h)2+k的图像性质同步课时作业(3)

试卷更新日期：2018-09-18 类型：同步测试

进入出卷网下载

一、选择题

1. 抛物线y=﹣（x﹣4）²﹣5的顶点坐标和开口方向分别是（）

A、（4，﹣5），开口向上 B、（4，﹣5），开口向下 C、（﹣4，﹣5），开口向上 D、（﹣4，﹣5），开口向下

查看试题解析
2. 已知二次函数 $y = a {(x + 3)}^{2} + b$ 有最大值0，则a，b的大小关系为（）

A、 $a$ ＜ $b$ B、 $a = b$ C、 $a$ ＞ $b$ D、大小不能确定

查看试题解析
3. 已知二次函数y=﹣（x﹣h）²+1（为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最大值为﹣5，则h的值为（）

A、3﹣ $\sqrt{6}$ 或1+ $\sqrt{6}$ B、3﹣ $\sqrt{6}$ 或3+ $\sqrt{6}$ C、3+ $\sqrt{6}$ 或1﹣ $\sqrt{6}$ D、1﹣ $\sqrt{6}$ 或1+ $\sqrt{6}$

查看试题解析
4. 把抛物线 $y = x + 1^{2}$ 向下平移2个单位，再向右平移1个单位，所得到的抛物线是（）

A、 $y = x + 2^{2} + 2$ B、 $y = x + 2^{2} - 2$ C、 $y = x^{2} + 2$ D、 $y = x^{2} - 2$

查看试题解析
5. 已知二次函数y=3（x+1）²﹣8的图象上有三点A（1，y₁），B（2，y₂），C（﹣2，y₃），则y₁ ， y₂ ， y₃的大小关系为（）

A、y₁＞y₂＞y₃ B、y₂＞y₁＞y₃ C、y₃＞y₁＞y₂ D、y₃＞y₂＞y₁

查看试题解析
6. 已知直线y=﹣ $\sqrt{3}$ x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣ $\frac{1}{3}$ （x﹣ $\sqrt{3}$ ）²+4上，能使△ABP为等腰三角形的点P的个数有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

7. 抛物线y=2（x+2）²+4的顶点坐标为．

查看试题解析
8. 已知点A（x₁ ， y₁）和B（x₂ ， y₂）是抛物线y=2（x﹣3）²+5上的两点，如果x₁＞x₂＞4，那么y₁y₂ ．（填“＞”、“=”或“＜”）

查看试题解析
9. 在平面直角坐标系xOy中，将抛物线 $y = 3 {(x + 2)}^{2} - 1$ 平移后得到抛物线 $y = 3 x^{2} + 2$ .请你写出一种平移方法. 答：.

查看试题解析
10. 把抛物线y=﹣x²先向上平移2个单位，再向左平移3个单位，所得的抛物线是．

查看试题解析
11. 若抛物线y=(x-m) $^{2}$ +(m+1)的顶点在第一象限，则m的取值范围为.

查看试题解析
12. 如图，抛物线y₁=a（x+2）²﹣3与y₂= $\frac{1}{2}$ （x﹣3）²+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：
①无论x取何值，y₂的值总是正数；
②a=1；
③当x=0时，y₂﹣y₁=4
④2AB=3AC．
其中正确结论是．

查看试题解析

三、解答题

13. 用配方法把二次函数 $y = - 2 x^{2} + 6 x + 4$ 化为 $y = a {(x + m)}^{2} + k$ 的形式，再指出该函数图象的开口方向、对称轴和顶点坐标.

查看试题解析
14. 已知二次函数的图象的顶点坐标为（﹣2，﹣3），且图象过点（﹣3，﹣1），求这个二次函数的解析式．

查看试题解析
15. 如图是二次函数y＝a(x＋1)²＋2的图象的一部分，根据图象回答下列问题：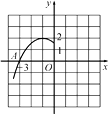

(1)、抛物线与x轴的一个交点A的坐标是，则抛物线与x轴的另一个交点B的坐标是；

(2)、确定a的值；

(3)、设抛物线的顶点是P，试求△PAB的面积．

查看试题解析
16. 在直角坐标系中，二次函数图象的顶点为A（1、﹣4），且经过点B（3，0）．

(1)、求该二次函数的解析式；

(2)、当﹣3＜x＜3时，函数值y的增减情况；

(3)、将抛物线怎样平移才能使它的顶点为原点．

查看试题解析
17. 已知：抛物线 $y = \frac{3}{4} {(x - 1)}^{2} - 3$ ．

(1)、写出抛物线的开口方向、对称轴；

(2)、函数y有最大值还是最小值？并求出这个最大（小）值；

(3)、设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．

查看试题解析