2018-2019学年数学浙教版八年级上册 第二章 特殊三角形 单元测试卷
试卷更新日期：2018-09-18 类型：单元试卷
一、选择题
-
1. Rt△ABC中，∠C=90°，∠B=36°，则∠A=（ ）A、44° B、34° C、54° D、64°2. 已知x、y为正数，且|x﹣4|+（y﹣3）2=0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为直径的圆的面积为（ ）A、5π B、25π C、7π D、6.25π3. 如图，将∠BAC沿DE向∠BAC内折叠，使AD与A′D重合，A′E与AE重合，若∠A=30°，则∠1+∠2=（ ）
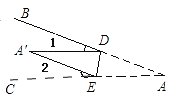A、50° B、60° C、45° D、以上都不对4. 在△ABC中，∠B=30°，点D在BC边上，点E在AC边上，AD=BD，DE=CE，若△ADE为等腰三角形，则∠C的度数为（ ）
A、20° B、20°或30° C、30°或40° D、20°或40°5. 如图，在4×4方格中，以AB为一边，第三个顶点也在格点上的等腰三角形可以作出（ ）
A、7个 B、6个 C、4个 D、3个6. 如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A对应点为A′，且B′C=3，则AM的长是（ ）
A、1.5 B、2 C、2.25 D、2.57. 如图是我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形、如果大正方形的面积13，小正方形的面积是1，直角三角形的短直角边为a，较长的直角边为b，那么（a+b）2的值为（ ）
A、169 B、25 C、19 D、138. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）2=21，大正方形的面积为13，则小正方形的面积为（ ）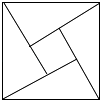
A、3 B、4 C、5 D、69. 历史上对勾股定理的一种证法采用了下列图形：其中两个全等的直角三角形边AE、EB在一条直线上．证明中用到的面积相等关系是（ ）
A、S△EDA=S△CEB B、S△EDA+S△CEB=S△CDB C、S四边形CDAE=S四边形CDEB D、S△EDA+S△CDE+S△CEB=S四边形ABCD10.在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图的直角梯形，其中三边长分别为 ， 3，4，则原直角三角形纸片的斜边长是（ ）
A、10 B、3 C、10或3 D、10或2二、填空题
-
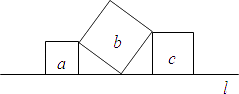
11. 等腰三角形的一个内角为70°，它一腰上的高与底边所夹的度数为 ．12. 如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为 ．
13. 如图，在△ABC中，D为AB上一点，AD=CD=BC，若∠ACD=40°，则∠B=°．
14. 一个三角形有一内角为48°，如果经过其一个顶点作直线能把其分成两个等腰三角形，那么它的最大内角可能是 ．15. 如图所示，已知△ABC中，∠ACB=90°，AB=5cm，BC=3cm，CD⊥AB于D，则CD的长为cm．
16. 如图，将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F点处，已知DE=5，AB=8，则BF= ．
17. 如图，A、B是网格中的两个格点，点C也是网格中的一个格点，连接AB、BC、AC，当△ABC为等腰三角形时，格点C的不同位置有处，设网格中的每个小正方形的边长为1，则所有满足题意的等腰三角形ABC的面积之和等于 ．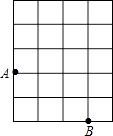
18. 如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A1处，称为第1次操作，折痕DE到BC的距离记为h1 ， 还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2；按上述方法不断操作下去…，经过第2017次操作后得到的折痕D2016E2016 ， 到BC的距离记为h2017；若h1=1，则h2017的值为 ．
三、解答题
-
19. 在Rt△ABC中，∠C=90°，∠A=2∠B，求出∠A，∠B的度数．20. 阅读下列材料，并回答问题． 事实上，在任何一个直角三角形中，两条直角边的平方之和一定等于斜边的平方，这个结论就是著名的勾股定理．请利用这个结论，完成下面活动：
(1)、一个直角三角形的两条直角边分别为6、8，那么这个直角三角形斜边长为(2)、如图1，AD⊥BC 于D，AD=BD，AC=BE，AC=3，DC=1，求BD的长度．(3)、如图2，点A在数轴上表示的数是 ， 请用类似的方法在图2数轴上画出表示数 的B点（保留作图痕迹）．
21. 已知：△ABC中，∠B、∠C的角平分线相交于点D，过D作EF∥BC交AB于点E，交AC于点F，求证：BE+CF=EF．
22. 如图：E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F，DF=EF，BD=CE．求证：△ABC是等腰三角形．（过D作DG∥AC交BC于G）
23. ABCD是长方形纸片的四个顶点，点E、F、H分别是边AB、BC、AD上的三点，连结EF、FH．
(1)、将长方形纸片的ABCD按如图①所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′，点B′在F C′上，则∠EFH的度数为；
(2)、将长方形纸片的ABCD按如图②所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′（B′、C′的位置如图所示），若∠B′FC′=18°，求∠EFH的度数；
(3)、将长方形纸片的ABCD按如图③所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B′、C′、D′（B′、C′的位置如图所示），若∠EFH=β°，求∠B′FC′的度数为 ．
24. 如图1，△ABC中，CD⊥AB于D，且BD：AD：CD=2：3：4，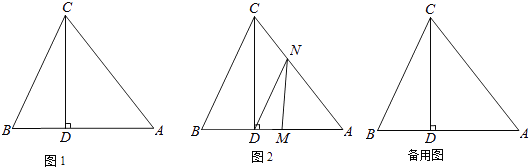
(1)、试说明△ABC是等腰三角形；(2)、已知S△ABC=40cm2 ， 如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止．设点M运动的时间为t（秒），①若△DMN的边与BC平行，求t的值；
②若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，求出t的值；若不能，请说明理由．