2018-2019学年数学人教版（五四学制）八年级上册20.1.2线段的垂直平分线 同步练习
试卷更新日期：2018-09-18 类型：同步测试
一、选择题
-
1. 如图，在 Rt△ABC中，∠C=90°，AC=3，BC=4，AB的垂直平分线交BC于点D，连接AD，则△ACD的周长是（ ）
A、7 B、8 C、9 D、102. 如图，已知 是 的角平分线， 是 的垂直平分线， ， ，则 的长为（ ）
A、6 B、5 C、4 D、3. 如图，在△ABC中，DE垂直平分AB，交边AC于点D，交边AB于点E，连接BD．若AC=6，△BCD的周长为10，则BC的长为（ ）
A、2 B、4 C、6 D、84. 如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点．已知△PAB的周长为14，PA＝4，则线段AB的长度为（ ）
A、6 B、5 C、4 D、35. 已知点 在线段 的中垂线上，点 在线段 的中垂线外，则（ ）．A、 B、 C、 D、不能确定6. 如图，∠AOB和线段CD，如果P点到OA，OB的距离相等，且PC=PD，则P点是（ ）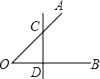
A、∠AOB的平分线与CD的交点 B、CD的垂直平分线与OA的交点 C、∠AOB的平分线与CD的垂直平分线的交点 D、CD的中点7. 如图，在 中， ， 的平分线AD交BC于点D，若DE垂直平分AB，则 的度数为（ ）
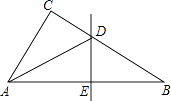A、 B、 C、 D、8. 如图，在△ABC中，分别以点A和点C为圆心，大于
AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（ ）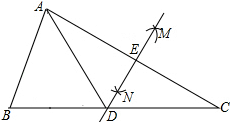
A、16cm B、19cm C、22cm D、25cm9. 如图，DE是△ABC中AC边的垂直平分线，若BC=8，AB=10，则△EBC的周长为（ ）．
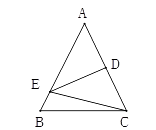A、16 B、18 C、26 D、2810. 如图，在△ABC中，∠A=36°，AB=AC，AB的垂直平分线OD交AB于点O，交AC于点D，连接BD．有下列结论：①∠C=2∠A；②BD平分∠ABC；③S△BCD=S△BOD．其中正确的选项是（ ）
A、①③ B、②③ C、①②③ D、①②二、填空题
-
11. 小军做了一个如图所示的风筝，其中EH=FH，ED=FD，小军说不用测量就知道DH是EF的垂直平分线．其中蕴含的道理是
12. 如图，CD是线段AB的垂直平分线，若AC=2cm，BD=4cm，则四边形ACBD的周长是cm．
13. 如图，△ABC中，BC的垂直平分线l与AC相交于点D，若△ABD的周长为6cm，则AB+AC=cm.
14. 如图所示，在△ABC中，DM，EN分别垂直平分AB和AC，交BC于点D，E，若△ADE的周长为19 cm，则BC＝
15. 如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于 BC的长为半径作弧，两弧相交于M，N两点；②作直线MN交AB于点D，连接CD.若CD＝AC，∠B＝25°，则∠ACB的度数为 ． 
16. 如图所示，已知线段AB=6，现按照以下步骤作图：①分别以点A，B为圆心，以大于 AB的长为半径画弧，两弧相交于点C和点D；
②连结CD交AB于点P．
则线段PB的长为 ．
三、解答题
-
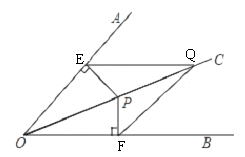
17. 已知：OC平分∠AOB，点P、Q都是OC上不同的点，PE⊥OA，PF⊥OB，垂足分别为E、F，连接EQ、FQ.求证：FQ＝EQ
18. 如图，在△ABC中，AB的垂直平分线ED交AC于D，如果AC=7，BC=5，求△BDC的周长．
19. 如图，已知∠BAC=60° ，∠B=80° ，DE垂直平分AC交BC于点D，交AC于点E.
(1)、求∠BAD的度数；
(2)、若AB=10，BC=12，求△ABD的周长.
