2018-2019学年数学浙教版九年级上册二次函数图象与系数的关系
试卷更新日期:2018-09-18 类型:同步测试
一、选择题
-
1. 二次函数 的图象一定不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限.2. 已知二次函数y=ax2+bx+c的图象大致如图所示,则下列关系式中成立的是( )
 A、a>0 B、b<0 C、c<0 D、b+2a>03. 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有( )
A、a>0 B、b<0 C、c<0 D、b+2a>03. 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有( ) A、0个 B、1个 C、2个 D、3个4. 二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+a的图象大致是( )
A、0个 B、1个 C、2个 D、3个4. 二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+a的图象大致是( ) A、
A、 B、
B、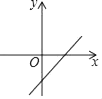 C、
C、 D、
D、 5. 二次函数y=x2+4x﹣5的图象的对称轴为( )A、x=﹣4 B、x=4 C、x=﹣2 D、x=26. 二次函数y=ax2+bx+c(a≠0)的图象如图,
5. 二次函数y=x2+4x﹣5的图象的对称轴为( )A、x=﹣4 B、x=4 C、x=﹣2 D、x=26. 二次函数y=ax2+bx+c(a≠0)的图象如图,
下列结论:(1)c<0;(2)b>0;(3)4a+2b+c>0;(4)(a+c)2<b2
其中不正确的有( )A、1个 B、2个 C、3个 D、4个7. 如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么下列不等式成立的是( )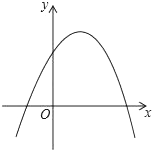 A、a>0 B、b<0 C、ac<0 D、bc<0.8. 抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
A、a>0 B、b<0 C、ac<0 D、bc<0.8. 抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )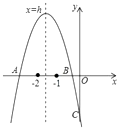 A、①②③④ B、①②④ C、①③④ D、①②③9. 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).关于这个二次函数的描述:① a<0,b>0,c<0;② 当x=2时,y的值等于1;③ 当x>3时,y的值小于0.正确的是( )
A、①②③④ B、①②④ C、①③④ D、①②③9. 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).关于这个二次函数的描述:① a<0,b>0,c<0;② 当x=2时,y的值等于1;③ 当x>3时,y的值小于0.正确的是( )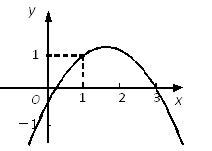 A、①② B、①③ C、②③ D、①②③10. 如图,抛物线 (a≠0)的对称轴为直x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ;②方程 =0的两个根是 ③ ;④当 时,x的取值范围是 ;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
A、①② B、①③ C、②③ D、①②③10. 如图,抛物线 (a≠0)的对称轴为直x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ;②方程 =0的两个根是 ③ ;④当 时,x的取值范围是 ;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有实数根,则m的最小值为 .
 12. 如图所示的抛物线y=x2+bx+b2﹣4的图象,那么b的值是 .
12. 如图所示的抛物线y=x2+bx+b2﹣4的图象,那么b的值是 .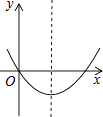 13. 抛物线y=ax2+bx(a>0,b>0)的图象经过第象限.14. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:
13. 抛物线y=ax2+bx(a>0,b>0)的图象经过第象限.14. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3③a+b+c>0④当x>1时,y随x的增大而增大.正确的说法有 .
 15. 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0 ②b<0 ③c>0 ④4a+2b+c=0, ⑤b+2a=0 ⑥ b2-4ac>0其中正确的是 . (写出所有正确结论的序号)
15. 二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0 ②b<0 ③c>0 ④4a+2b+c=0, ⑤b+2a=0 ⑥ b2-4ac>0其中正确的是 . (写出所有正确结论的序号) 16. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ① c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am +bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y )在该抛物线上,则y>y .其中正确的结论有 .(写出所有正确结论的序号)
16. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ① c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am +bm+a>0(m≠﹣1);⑤设A(100,y),B(﹣100,y )在该抛物线上,则y>y .其中正确的结论有 .(写出所有正确结论的序号)
三、解答题
-
17. 已知抛物线y=ax2+bx+c的大致图象如图所示,试确定a,b,c,b2-4ac及a+b+c的符号.
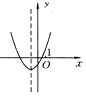 18. 已知二次函数y=x2-2x-3.(1)、用配方法将表达式化为y=(x-h)2+k的形式;(2)、求这个函数图象与x轴的交点坐标.19. 二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,试判断P,Q的大小关系.
18. 已知二次函数y=x2-2x-3.(1)、用配方法将表达式化为y=(x-h)2+k的形式;(2)、求这个函数图象与x轴的交点坐标.19. 二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,试判断P,Q的大小关系.