2018-2019学年数学浙教版九年级上册2.3用频率估计概率 同步练习
试卷更新日期：2018-09-18 类型：同步测试
一、选择题
-
1. 在一个不透明的盒子里有n个除颜色外其他均相同的小球，其中有8个黄球，采用有放回的方式摸球，结果发现摸到黄球的频率稳定在40%，那么可以推算出n大约是（ ）
A、8 B、20 C、32 D、402. 下表记录了一名球员在罚球线上投篮的结果，这名球员投篮一次，投中的概率约是（ ）投篮次数
10
50
100
150
200
250
300
500
投中次数
4
35
60
78
104
123
151
249
投中频率
0.40
0.70
0.60
0.52
0.52
0.49
0.51
0.50
A、0.5 B、0.7 C、0.6 D、0.43. 在一个不透明的盒子中装有a个除颜色外完全相同的球，这a个球中只有3个红球，若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子.通过大量重复试验后，发现摸到红球的频率稳定在0. 2左右，则a的值约为 （ ）
A、12 B、15 C、18 D、204. 小明练习射击，共射击60次，其中有38次击中靶子，由此可估计，小明射击一次击中靶子的频率约是（ ）
A、38% B、60% C、63% D、无法确定5. 小红把一枚硬币抛掷10次，结果有4次正面朝上，那么（ ）A、正面朝上的频数是0.4 B、反面朝上的频数是6 C、正面朝上的频率是4 D、反面朝上的频率是66. 做重复试验：抛掷同一枚啤酒瓶盖1000次．经过统计得“凸面向上”的次数约为420次，则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为（ ）A、0.22 B、0.42 C、0.50 D、0.587. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下折线统计图，则符合这一结果的实验最有可能的是（ ）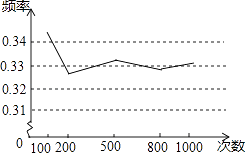
A、袋中装有大小和质地都相同的3个红球和2个黄球，从中随机取一个，取到红球 B、掷一枚质地均匀的正六面体骰子，向上的面的点数是偶数 C、先后两次掷一枚质地均匀的硬币，两次都出现反面 D、先后两次掷一枚质地均匀的正六面体骰子，两次向上的面的点数之和是7或超过98. 某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（ ）
A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球二、填空题
-
9. 在创建国家生态园林城市活动中，某市园林部门为了扩大城市的绿化面积，进行了大量的树木移栽．下表记录的是在相同的条件下移栽某种幼树的棵数与成活棵数：
移栽棵数
100
1 000
10 000
成活棵数
89
910
9 008
依此估计这种幼树成活的概率是 ． (结果用小数表示，精确到0.1)
10. 在研究抛掷分别标有1，2，3，4，5，6的质地均匀的正六面体骰子时，提出了一个问题：连续抛掷三次骰子，正面朝上的点数是三个连续整数的概率有多大，假设下表是几位同学抛掷骰子的试验数据.请你根据这些数据估计上面问题的答案大约是.(精确到0.01)投掷次数
投掷情况
1
2
3
4
5
6
7
8
试验次数
100
150
200
250
300
350
400
450
三个连续正数的次数
10
12
20
22
25
33
36
41
11. 在进行某批乒乓球的质量检验时，当抽取了2000个乒乓球时，发现优等品有1898个，则这批乒乓球“优等品”的概率的估计值是（精确到0.01）.
12. 下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果. 随着实验次数的增加，“钉尖向上”的频率总在一常数附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是
13. 某商店进行“迎五一，大促销”摸奖活动，凡是有购物小票的顾客均可摸球一次，摸到的是白球即可获奖．规则如下：一个不透明的袋子中装有10个黑球和若干白球，它们除颜色不同外，其余均相同，从袋子中随机摸出一个球，记下颜色，再把它放回袋子中摇匀，重复此过程．共有300人摸球，其中获奖的共有180人，由此估计袋子中白球大约有个．
14. 某射手在相同条件下进行射击训练，结果如下：射击次数n
10
20
40
50
100
200
500
1000
击中靶心的频数m
9
19
37
45
89
181
449
901
击中靶心的频率
0.900
0.950
0.925
0.900
0.890
0.905
0.898
0.901
该射手击中靶心的概率的估计值是（精确到0.01）．
15. 从甲地到乙地有A，B，C三条不同的公交线路．为了解决早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：公交车用时
公交车用时的频数
线路
合计
A
59
151
166
124
500
B
50
50
122
278
500
C
45
265
167
23
500
早高峰期间，乘坐（填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．
16. 下表记录了某种幼树在一定条件下移植成活情况移植总数n
400
1500
3500
7000
9000
14000
成活数m
325
1336
3203
6335
8073
12628
成活的频率（精确到0.01）
0.813
0.891
0.915
0.905
0.897
0.902
由此估计这种幼树在此条件下移植成活的概率约是（精确到0.1）
三、解答题
-
17. 某人承包了一池塘养鱼，他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼，把每条鱼都作上标记，放回鱼塘；过了2天，他让他父亲从鱼塘内打捞上了50条鱼，结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤，平均每条鱼估计2.3斤，你能帮助他估计一下今年的收入情况吗?
18. 小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）试验，她们共做了60次试验，试验的结果如下：朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)、计算“3点朝上”的频率和“5点朝上”的频率.
(2)、小颖说：“根据上述试验，一次试验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
19. 某商场设立了一个可以自由转动的转盘(如图)，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是活动进行中的一组统计数据：
(1)、计算并完成表格：转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”的次数m
68
111
136
345
546
701
落在“铅笔”的频率
(2)、假如你去转动该转盘一次，你获得铅笔的概率约是多少？
20. 某生活小区鲜奶店每天以每瓶3元的价格从奶场购进优质鲜奶，然后以每瓶6元的价格出售，如果当天卖不完，剩余的只有倒掉．店主记录了30天的日需求量（单位：瓶），整理得下表：日需求量
26
27
28
29
30
频数
5
8
7
6
4
(1)、求这30天内日需求量的众数；
(2)、假设鲜奶店在这30天内每天购进28瓶，求这30天的日利润（单位：元）的平均数；(3)、以30记录的各需求量的频率作为各需求是发生的概率．若鲜奶店每天购进28瓶，求在这记录的30天内日利润不低于81元的概率．
21. 在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球试验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图.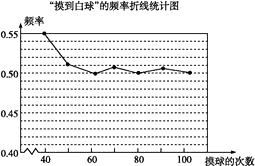
(1)、请估计：当n足够大时，摸到白球的频率将会稳定在(精确到0.01)，假如你摸一次，你摸到白球的概率为；
(2)、试估算盒子里白、黑两种颜色的球各有多少个?
(3)、在(2)条件下如果要使摸到白球的概率为 ，需要往盒子里再放入多少个白球?
22. 在一个不透明的口袋里装有只有颜色不同的黑、白两种球共20个，某学习小组做摸球实验，每次摸出一个球再把它放回袋中，不断重复，下表是一次摸球实验的一组统计数据．摸球的次数n
100
150
200
500
800
1 000
摸到白球的次数m
58
96
116
295
484
601
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.601
(1)、请估计：当n很大时，摸到白球的频率将会接近多少？
(2)、试估算口袋里黑、白两种颜色的球各有多少个？