2018-2019学年数学浙教版九年级上册2.2 简单事件的概率（1） 同步练习
试卷更新日期：2018-09-18 类型：同步测试
一、选择题
-
1. 小明做了6次掷质地均匀硬币的试验，在前 5 次试验中，有 2 次正面朝上，3 次正面朝下， 那么第 6 次试验，硬币正面朝上的概率是（ ）A、1 B、0 C、0.5 D、不稳定2. 一只小狗在如图的方砖上走来走去，最终停在阴影方砖上的概率是（ ）
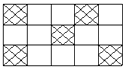A、 B、 C、 D、3. 一个不透明的盒子里有9个黄球和若干个红球，红球和黄球除颜色外其他完全相同，每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球试验后发现，摸到黄球的频率稳定在30%，那么估计盒子中红球的个数为（ ）
A、11 B、15 C、19 D、214. 在一个不透明的袋子里装着9个完全相同的乒乓球，把它们分别标记上数字1，2，3，4，5，6，7，8，9，从中随机摸出一个小球，标号为奇数的概率为（ ）
A、 B、 C、 D、5. 在一个暗箱内放有a个除颜色外其余完全相同的小球，其中红球只有3个且摸到红球的概率为15%，则a的值是（ ）
A、20 B、15 C、12 D、96. 四张相同的卡片，每张的正面分别写着 ， ， ， ，将卡片正面朝下扣在桌上，随机抽出一张，这张卡片上写的不是最简二次根式的概率是（ ）
A、 B、 C、 D、7. 小明向图中的格盘中随意掷一棋子，使之落在三角形内的概率是（ ）
A、 B、 C、 D、8. 一个不透明的盒子中，放着编号为1到10的10张卡片（编号均为正整数），这些卡片除了编号以外没有任何其他区别．盒中卡片已经搅匀，从中随机的抽出一张卡片，则“该卡片上的数字大于 ”的概率是（ ）
A、 B、 C、 D、9. 笔筒中有10支型号、颜色完全相同的铅笔，将它们逐一标上1﹣10的号码，若从笔筒中任意抽出一支铅笔，则抽到编号是3的倍数的概率是（ ）
A、 B、 C、 D、10. 掷一枚均匀的骰子，骰子的6个面上分别刻有1、2、3、4、5、6点，则点数为奇数的概率是（ ）A、 B、 C、 D、二、填空题
-
11. 张华讲义夹里放了大小相同的试卷共12张，其中语文4张、数学2张、英语3张、物理3张，他随机地从讲义夹中抽出1张，抽出的试卷恰好是数学试卷的概率为 ．
12. 在一张边长为4cm的正方形纸上做扎针随机试验，纸上有一个半径为1cm的圆形阴影区域，则针头扎在阴影区域内的概率为；
13. 袋子里有6只红球，4只白球，每只球除颜色以外都相同，从中任意摸出1只球，是红的可能性 选填“大于”“小于”或“等于”)是白球的可能性．
14. 有四张看上去无差别的卡片，正面分别写有“兴城首山”、“龙回头”、“觉华岛”、“葫芦山庄”四个景区的名称，将它们背面朝上，从中随机一张卡片正面写有“葫芦山庄”的概率是 ．
15. 已知函数y=（2k﹣1）x+4（k为常数），若从﹣3≤k≤3中任取k值，则得到的函数是具有性质“y随x增加而增加”的一次函数的概率为 ．
16. 如图，这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．已知AE=3，BE=2，若向正方形ABCD内随意投掷飞镖（每次均落在正方形ABCD内，且落在正方形ABCD内任何一点的机会均等），则恰好落在正方形EFGH内的概率为 ．
17. 如图，正六边形内接于⊙O，小明向圆内投掷飞镖一次，则飞镖落在阴影部分的概率是 ．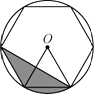
三、解答题
-
18. “十一”黄金周期间，某购物广场举办迎国庆有奖销售活动，每购物满100元，就会有一次转动大转盘的机会，请你根据大转盘(如图)来计算：
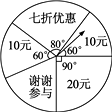(1)、享受七折优惠的概率；
(2)、得20元的概率；
(3)、得10元的概率；(4)、中奖得钱的概率是多少？
19. 有7张卡片，分别写有数字 -1，0，1，2，3，4，5，这七个数字，从中任意抽取一张，
(1)、求抽到的数字为正数的概率(2)、求抽到数字的绝对值小于2的概率.
20. 米奇家住宅面积为90平方米，其中客厅30平方米，大卧室18平方米，小卧室15平方米，厨房14平方米，大卫生间9平方米，小卫生间4平方米．如果一只小猫在该住宅内地面上任意跑．求：
(1)、P(在客厅捉到小猫)；(2)、P(在小卧室捉到小猫)；(3)、P(在卫生间捉到小猫)；(4)、P(不在卧室捉到小猫)．
21. 6月14日是“世界献血日”，某市采取自愿报名的方式组织市民义务献血．献血时要对献血者的血型进行检测，检测结果有“A型”、“B型”、“AB型”、“O型”4种类型．在献血者人群中，随机抽取了部分献血者的血型结果进行统计，并根据这个统计结果制作了两幅不完整的图表：血型
A
B
AB
O
人数
10
5
(1)、这次随机抽取的献血者人数为人，m=；(2)、补全上表中的数据；(3)、若这次活动中该市有3000人义务献血，请你根据抽样结果回答：从献血者人群中任抽取一人，其血型是A型的概率是多少？并估计这3000人中大约有多少人是A型血？
22. 杨老师为了了解所教班级学生课后复习的具体情况，对本班部分学生进行了一个月的跟踪调查，然后将调查结果分成四类：A：优秀；B：良好；C：一般；D：较差．并将调查结果绘制成以下两幅不完整的统计图．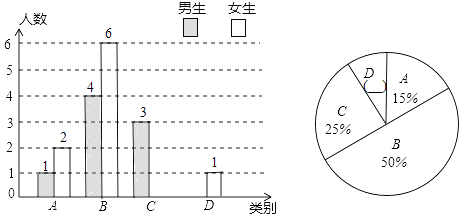
请根据统计图解答下列问题：
(1)、本次调查中，杨老师一共调查了名学生，其中C类女生有名，D类男生有名；
(2)、补全上面的条形统计图和扇形统计图；
(3)、在此次调查中，小平属于D类．为了进步，她请杨老师从被调查的A类学生中随机选取一位同学，和她进行“一帮一”的课后互助学习．请求出所选的同学恰好是一位女同学的概率．