2018-2019学年数学苏科版九年级上册第1章一元二次方程单元检测

试卷更新日期：2018-09-13 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列方程中不一定是一元二次方程的是（）.

A、 $(a - 3) x^{2} = 8 (a \neq 3)$ B、 $a x^{2} + b x + c = 0$ C、 $（ x + 3) (x - 2) = x + 5$ D、 $\sqrt{3} x^{2} + \frac{3}{57} x- 2 = 0$

查看试题解析
2. 关于x的一元二次方程（m-1）x²+5x+m²-3m+2=0的常数项是0，则m的值（）

A、1 B、1或2 C、2 D、±1

查看试题解析
3. 把方程x（x+2）=5（x﹣2）化成一般式，则a、b、c的值分别是（　　）

A、1，﹣3，10 B、1，7，﹣10 C、1，﹣5，12 D、1，3，2

查看试题解析
4. 已知a，b是关于x的一元二次方程x²+nx﹣1=0的两实数根，则式子 $\frac{b}{a} + \frac{a}{b}$ 的值是（）

A、n²+2 B、﹣n²+2 C、n²﹣2 D、﹣n²﹣2

查看试题解析
5. 下列方程能直接开平方的是（　　）

A、5x²+2=0 B、4x²﹣2x+1=0 C、（x﹣2）²=4 D、3x²+4=2

查看试题解析
6. 对于代数式﹣x²+4x﹣5，通过配方能说明它的值一定是（）

A、非正数 B、非负数 C、正数 D、负数

查看试题解析
7. 用公式法解﹣x²+3x=1时，先求出a、b、c的值，则a、b、c依次为（　　）

A、﹣1，3，﹣1 B、1，﹣3，﹣1 C、﹣1，﹣3，﹣1 D、﹣1，3，1

查看试题解析
8. 若方程x²﹣（m²﹣4）x+m=0的两个根互为相反数，则m等于（）

A、﹣2 B、2 C、±2 D、4

查看试题解析
9. 一元二次方程式x²﹣8x=48可表示成（x﹣a）²=48+b的形式，其中a、b为整数，求a+b之值为何（）

A、20 B、12 C、﹣12 D、﹣20

查看试题解析
10. 一元二次方程x²﹣6x﹣5=0配方可变形为（）

A、（x﹣3）²=14 B、（x﹣3）²=4 C、（x+3）²=14 D、（x+3）²=4

查看试题解析
11. 下列方程不适于用因式分解法求解的是（）

A、x²﹣（2x﹣1）²=0 B、x（x+8）=8 C、2x（3﹣x）=x﹣3 D、5x²=4x

查看试题解析
12. 以x= $\frac{b \pm \sqrt{b^{2} - 4 c}}{2}$ 为根的一元二次方程可能是（　　）

A、 $x^{2}$ +bx+c=0 B、 $x^{2}$ +bx﹣c=0 C、 $x^{2}$ ﹣bx+c=0 D、 $x^{2}$ ﹣bx﹣c=0

查看试题解析
13. 将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形，做成一个无盖的盒子，已知盒子的容积为300cm³ ，则原铁皮的边长为（　　）

A、10cm B、13cm C、14cm D、16cm

查看试题解析
14. 菱形ABCD的一条对角线长为6，边AB的长是方程x²﹣7x+12=0的一个根，则菱形ABCD的周长为（）

A、16 B、12 C、16或12 D、24

查看试题解析
15. 若实数范围内定义一种运算“﹡”，使a*b=（a+1）²﹣ab，则方程（x+2）*5=0的解为（　　）

A、-2 B、﹣2，3 C、 $\frac{- 1 + \sqrt{3}}{2}$ , $\frac{- 1 - \sqrt{3}}{2}$ D、 $\frac{- 1 + \sqrt{5}}{2}$ , $\frac{- 1 - \sqrt{5}}{2}$

查看试题解析

二、填空题

16. 已知x= $\frac{- b + \sqrt{b^{2} - 4 c}}{2}$ （b²﹣4c＞0），则x²+bx+c的值为．

查看试题解析
17. 已知三角形两边长是方程x²﹣5x+6=0的两个根，则三角形的第三边c的取值范围是．

查看试题解析
18. 方程2x²+3x﹣1=0的两个根为x₁、x₂ ，则 $\frac{1}{x_{1}}$ + $\frac{1}{x_{2}}$ 的值等于．

查看试题解析
19. 方程2x²﹣6x﹣5=0两根为α，β，则α²+β²= ，（α﹣β）²= ．

查看试题解析
20. 现定义运算“★”，对于任意实数a、b，都有a★b=a²﹣3a+b，如：3★5=3²﹣3×3+5，若x★2=6，则实数x的值是．

查看试题解析

三、计算题

21. 解下列方程：

(1)、x²﹣4x+4=0

(2)、x（x﹣2）=3（x﹣2）

(3)、（2y﹣1）²﹣4=0

(4)、（2x+1）（x﹣3）=0

(5)、x²+5x+3=0

(6)、x²﹣6x+1=0．

查看试题解析

四、综合题

22. 关于x的一元二次方程x²﹣6x+p²﹣2p+5=0的一个根为2．

(1)、求p值．

(2)、求方程的另一根．

查看试题解析
23. 某中心城市有一楼盘，开发商准备以每平方米7000元价格出售，由于国家出台了有关调控房地产的政策，开发商经过两次下调销售价格后，决定以每平方米5670元的价格销售．

(1)、求平均每次下调的百分率；

(2)、房产销售经理向开发商建议：先公布下调5%，再下调15%，这样更有吸引力，请问房产销售经理的方案对购房者是否更优惠？为什么？

查看试题解析
24. 某种商品的标价为400元/件，经过两次降价后的价格为324元/件，并且两次降价的百分率相同．

(1)、求该种商品每次降价的百分率；

(2)、若该种商品进价为300元/件，两次降价共售出此种商品100件，为使两次降价销售的总利润不少于3210元．问第一次降价后至少要售出该种商品多少件？

查看试题解析
25. 在一块长方形镜面玻璃的四周镶上与它的周长相等的边框，制成一面镜子，镜子的长与宽的比是2：1，设制作这面镜子的宽度是x米，总费用是y元，则y=240x²+180x+60．（注：总费用=镜面玻璃的费用+边框的费用+加工费）

(1)、这块镜面玻璃的价格是每平方米元，加工费元；

(2)、如果制作这面镜子共花了210元，求这面镜子的长和宽．

查看试题解析
26. 如图，A、B、C、D为矩形的四个顶点，AB=16cm，BC=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，点Q以2cm/s的速度向点D移动．当点P运动到点B停止时，点Q也随之停止运动．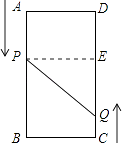

(1)、问几秒后，点P和点Q的距离是10cm？

(2)、问几秒后，以P、Q、D三点为顶点的三角形为直角三角形？
（提示：根据不同情况画出不同的图形，再给予解决问题．）

查看试题解析

2018-2019学年数学苏科版九年级上册 第1章 一元二次方程 单元检测

一、单选题

二、填空题

三、计算题

四、综合题

2018-2019学年数学苏科版九年级上册第1章一元二次方程单元检测