备考2019年高考数学一轮专题：第3讲简单的逻辑联结词、全称量词与存在量词

试卷更新日期：2018-09-12 类型：一轮复习

进入出卷网下载

一、单选题

1. 命题“方程x²=1的解是x=±1”中，使用逻辑词的情况是（）

A、没有使用逻辑联结词 B、使用了逻辑联结词“或” C、使用了逻辑联结词“且” D、使用了逻辑联结词“或”与“且”

查看试题解析
2. 如果命题“p且q”是假命题，“非p”是真命题，那么（）

A、命题p一定是真命题 B、命题q一定是真命题 C、命题q可以是真命题也可以是假命题 D、命题q一定是假命题

查看试题解析
3. 已知命题p：∃x₀∈R，tan x₀＝1，命题q：∀x∈R，x²＞0.下面结论正确的是（）

A、命题“p∧q”是真命题 B、命题“p∧( $\neg q$ )”是假命题 C、命题“( $\neg p$ )∨q”是真命题 D、命题“( $\neg p$ )∧( $\neg q$ )”是假命题

查看试题解析
4. 已知命题p：“∃x∈R，e^x－x－1≤0”，则﹁p为（）

A、∃x∈R，e^x－x－1≥0 B、∃x∈R，e^x－x－1＞0 C、∀x∈R，e^x－x－1＞0 D、∀x∈R，e^x－x－1≥0

查看试题解析
5. 命题“对任意的 $x \in R ， x^{2} + 2 x + 2 > 0$ ”的否定是（）

A、不存在 $x_{0} \in R ， x_{0}^{2} + 2 x_{0} + 2 \leq 0$ B、存在 $x_{0} \in R ， x_{0}^{2} + 2 x_{0} + 2 \leq 0$ C、存在 $x_{0} \in R ， x_{0}^{2} + 2 x_{0} + 2 > 0$ D、对任意的 $x \in R ， x^{2} + 2 x + 2 \leq 0$

查看试题解析
6. 已知命题“ $p$ 且 $q$ ”为真命题，则下面是假命题的是（）

A、 $p$ B、 $q$ C、 $p$ 或 $q$ D、 $\neg p$

查看试题解析
7. 已知命题 $p : \forall x > 0$ ，有 $e^{x} \geq 1$ 成立，则 $\neg p$ 为（）

A、 $\exists x_{0} \leq 0$ ，有 $e^{x_{0}} < 1$ 成立 B、 $\exists x_{0} \leq 0$ ，有 $e^{x_{0}} \geq 1$ 成立 C、 $\exists x_{0} > 0$ ，有 $e^{x_{0}} < 1$ 成立 D、 $\exists x_{0} > 0$ ，有 $e^{x_{0}} \leq 1$ 成立

查看试题解析
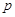8. 在一次跳高比赛前，甲、乙两名运动员各试跳了一次．设命题表示“甲的试跳成绩超过2米”，命题 $q$ 表示“乙的试跳成绩超过2米”，则命题 $p \lor q$ 表示（）

A、甲、乙恰有一人的试跳成绩没有超过2米 B、甲、乙至少有一人的试跳成绩没有超过2米 C、甲、乙两人的试跳成绩都没有超过2米 D、甲、乙至少有一人的试跳成绩超过2米

查看试题解析
9. 已知命题 $p ：$ 对任意 $x \in R$ ，总有 $2^{x} > 0$ ； $q ：$ “ $x > 1$ ”是“ $x > 2$ ”的充分不必要条件，则下列命题为真命题的是（）

A、 $p \land q$ B、 $\neg p \land \neg q$ C、 $\neg p \land q$ D、 $p \land \neg q$

查看试题解析
10. 已知命题 $p$ ：对任意 $x \in R$ ，都有 $e^{x} \leq 0$ ；命题 $q$ ：“ $x > 3$ ”是“ $x > 5$ ”的充分不必要条件，则下列命题为真命题的是（）

A、 $p \land q$ B、 $(\neg p) \land (\neg q)$ C、 $(\neg p) \land q$ D、 $p \land (\neg q)$

查看试题解析

二、填空题

11. 已知命题p：(x＋2)(x－6)≤0，命题q：－3≤x≤7，若“p或q”为真命题，“p且q”为假命题，则实数x的取值范围为．

查看试题解析
12. 设P：△ABC是等腰三角形；q：△ABC的直角三角形，则“p且q”形式的复合命题是

查看试题解析
13. 分别用“p或q”、“p且q”、“非p”填空：

①“菱形的对角线互相垂直平分”是形式；
②“负数没有平方根”是形式；
③“3≥3”是形式；
④“△ABC是等腰直角三角形”是形式

查看试题解析
14. 在一次跳伞训练中，甲、乙两位学员各跳一次，设命题p是“甲降落在指定范围”，q是“乙降落在指
定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为．

查看试题解析
15. 命题“ $\forall n \in N *$ ， $f (n) \in N *$ 且 $f (n) \leq n$ ”的否定为．

查看试题解析
16. 命题 $p : \exists x_{0} \in R$ ， $2^{x_{0}} \leq 0$ ，命题 $q : \forall x \in (0, \frac{π}{2}), x > \sin x$ ，其中真命题是；命题 $p$ 的否定是．

查看试题解析
17. 已知命题p：m∈R且m＋1≤0；命题q：∀x∈R，x²＋mx＋1>0恒成立．若p∧q为假命题，p $\lor$ q为真命题，则m的取值范围是．

查看试题解析

三、解答题

18. 已知命题 $p ： |x^{2} - x| \geq 6$ $q ： x \in z$ ，且“p且q”与“非q”同时为假命题，求x的值.

查看试题解析
19. 已知命题 p：方程 $a^{2} x^{2} + a x - 2 = 0 ；$ 在 $[- 1 ， 1]$ 上有且仅有一解；命题 q ：只有一个实数x满足不等式 $x^{2} + 2 a x + 2 a \leq 0$ .若命题“ p 或q ”是假命题，求a的取值范围．

查看试题解析
20. 已知 $p :$ 方程 $\frac{x^{2}}{m} + \frac{y^{2}}{m - 4} = 1$ 表示双曲线； $q :$ 方程 $\frac{x^{2}}{m^{2}} + \frac{y^{2}}{4} = 1$ 表示焦点在 $x$ 轴上的椭圆，若 $p \lor q$ 为真命题， $p \land q$ 为假命题，求实数 $m$ 的取值范围.

查看试题解析
21. 设命题 $p :$ 实数 $x$ 满足 $(x - a) (x - 3 a) < 0$ ，其中 $a > 0$ ，命题 $q$ ：实数 $x$ 满足 $\frac{x - 3}{x - 2} \leq 0$ ．

(1)、若 $a = 1$ ，且p∧q为真，求实数 $x$ 的取值范围；

(2)、若 ${}^{\neg}p$ 是 ${}^{\neg}q$ 的充分不必要条件，求实数 $a$ 的取值范围．

查看试题解析
22. 已知命题 $p :$ 方程 $x^{2} - 2 m x + m = 0$ 没有实数根；命题 $q : \forall x \in R, x^{2} + m x + 1 \geq 0$ .

(1)、写出命题 $q$ 的否定“ $\neg q$ ”.

(2)、如果“ $p \lor q$ ”为真命题，“ $p \land q$ ”为假命题，求实数 $m$ 的取值范围.

查看试题解析
23. 已知命题 $p :$ “存在 $x \in R, 2 x^{2} + (m - 1) x + \frac{1}{2} \leq 0$ ”，命题 $q$ ：“曲线 $C_{1} : \frac{x^{2}}{m^{2}} + \frac{y^{2}}{2 m + 8} = 1$ 表示焦点在 $x$ 轴上的椭圆”，命题 $s :$ “曲线 $C_{2} : \frac{x^{2}}{m - t} + \frac{y^{2}}{m - t - 1} = 1$ 表示双曲线”

(1)、若“ $p$ 且 $q$ ”是真命题，求实数 $m$ 的取值范围；

(2)、若 $q$ 是 $s$ 的必要不充分条件，求实数 $t$ 的取值范围.

查看试题解析

备考2019年高考数学一轮专题：第3讲 简单的逻辑联结词、全称量词与存在量词

一、单选题

二、填空题

三、解答题

备考2019年高考数学一轮专题：第3讲简单的逻辑联结词、全称量词与存在量词