新人教版数学八年级上册第十二章全等三角形12.3角的平分线的性质 同步练习
试卷更新日期：2015-08-12 类型：同步测试
一、选择题
-
1. 如图，∠1＝∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是（ ）A、PD＝PE B、OD＝OE C、∠DPO＝∠EPO D、PD＝OD
2. 如图，Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于D，若CD=6cm，则点D到AB的距离DE是（ ）
A、5cm B、4cm C、6cm D、2cm3. 如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC于点D，CD=2，则点D到AB的距离是 （ ）
A、1 B、2 C、3 D、44. 如图，已知AC⊥BC，DE⊥AB，AD平分∠BAC，下面结论错误的是（ ）
A、BD+ED=BC B、DE平分∠ADB C、AD平分∠EDC D、ED+AC＞AD5. 用尺规作已知角的平分线的理论依据是（ ）
A、SAS B、AAS C、SSS D、ASA6. 如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB＝6㎝，△DEB的周长为（ ）
A、4cm B、6cm C、10cm D、不能确定7. 已知如图△ABC中，AD是角平分线，AB=5，AC=3，且S△ADC=6，则S△ABD=
A、4 B、10 C、8 D、不能确定8. 到三角形三条边的距离都相等的点是这个三角形的（ ）A、三条中线的交点 B、三条角平分线的交点 C、三条边的垂直平分线的交点 D、三条高的交点9.如图，AD⊥OB ， BC⊥OA ， 垂足分别为D、C ， AD与BC相交于点P ， 若PA=PB ， 则∠1与∠2的大小是（ ）
A、∠1=∠2 B、∠1＞∠2 C、∠1＜∠2 D、无法确定10.如图，在Rt△ABC的斜边BC上截取CD=CA，过点D作DE⊥BC，交AB于E，则下列结论一定正确的是（ ）
A、AB=BE B、DB=DE C、AE=BD D、∠BCE=∠ACE11.如图，△ABC中，点O是△ABC内一点，且点O到△ABC三边的距离相等；∠A=40°，则∠BOC=（ ）
A、110° B、120° C、130° D、140°12.如图，△ABC的两个外角平分线交于点P，则下列结论正确的是（ ）
①PA=PC ②BP平分∠ABC ③P到AB，BC的距离相等 ④BP平分∠APC．
A、①② B、①④ C、②③ D、③④13.如图，DB⊥AB，DC⊥AC，BD=DC，∠BAC=80°，则∠BAD=（ ）．
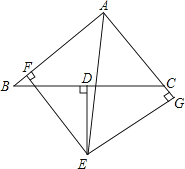
A、10° B、40° C、30° D、20°14.如图，已知AB∥CD，PE⊥AB，PF⊥BD，PG⊥CD，垂足分别E、F、G，且PF=PG=PE，则∠BPD=________．
A、60° B、70° C、80° D、90°15. 如图11.3-11，已知DB⊥AE于B，DC⊥AF于C，且DB=DC，∠BAC=40°，∠ADG=130°，则∠DGF=________．
A、130° B、150° C、100° D、140°二、填空题.
-
16.
如图所示，在△ABC中，∠C=90° ， AD平分∠BAC ， BC=20cm ， DB=17cm ， 则D点到AB的距离是cm．
17.如图所示，点D在AC上，∠BAD=∠DBC，△BDC的内部到∠BAD两边距离相等的点有个，△BDC内部到∠BAD的两边、∠DBC两边等距离的点有个．
18.如图，在△ABC中，∠A＝90°，BD平分∠ABC，AD＝2 cm，则点D到BC的距离为cm．
19. 如图， OP平分 ， 于点A，点Q是射线OM上一个动点，若PA=3，则PQ的最小值为 ．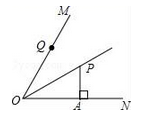
20. 如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是 ．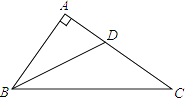
三、 证明题
-
21.
如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，AE=AF．求证：PE=PF；
22.如图，已知BD平分∠ABC，AB=BC，点P在BD上，PM⊥AD，PN⊥CD，M、N为垂足．求证：PM=PN．
