高中数学二轮复习

试卷更新日期：2017-03-01 类型：二轮复习

进入出卷网下载

一、单选题

1. 若关于x的不等式 $2 x^{2} - 8 x - 4 - a > 0$ 在 $1 < x < 4$ 内有解，则实数a的取值范围是（）

A、a<-12 B、a>-4 C、a>-12 D、a<-4

查看试题解析
2. 已知 ${(\sqrt{x} - \frac{a}{\sqrt{x}})}^{5}$ 的展开式中含 $x^{\frac{3}{2}}$ 的项的系数为30，则 $a$ =( )

A、 $\sqrt{3}$ B、 $\sqrt{- 3}$ C、6 D、- 6

查看试题解析
3. 设函数 $f (x) = \{\begin{matrix} 3 x - 1 ， x < 1 \\ 2^{x} ， x \geq 1 \end{matrix}$ ，则满足 $f (f (a)) = 2^{f (a)}$ 的 $a$ 取值范围是（）

A、 $[\frac{2}{3} ， 1]$ B、 $[0 ， 1]$ C、[ $\frac{2}{3} ， + \infty$ ) D、[ $1 ， + \infty$ )

查看试题解析
4. 已知全集 $U = \{1, 2, 3, 4, 5, 6\}$ ，集合 $A = \{2, 3, 5\}$ ，集合 $B = \{1,, 3, 4, 6\}$ ，则集合 $A \cap (C_{U} B) =$

A、 $\{3\}$ B、 $\{2, 5\}$ C、 $\{1, 4, 6\}$ D、 $\{2, 3, 5\}$

查看试题解析
5. 已知直线 $l$ : $x + a y - 1 = 0 (a \in R)$ 是圆 $C$ ： $x^{2} + y^{2} - 4 x - 2 y + 1 = 0$ 的对称轴。过点 $A (- 4, a)$ 作圆 $C$ 的一条切线，切点为B，则AB= （）

A、 $2$ B、 $4 \sqrt{2}$ C、 $6$ D、 $2 \sqrt{10}$

查看试题解析
6. 设函数f(x)=ln(1+x)-ln(1-x)，则f(x)是( )

A、奇函数，且在（0，1）上是增函数 B、奇函数，且在（0，1）上是减函数 C、偶函数，且在（0，1）上是增函数 D、偶函数，且在（0，1）上是减函数

查看试题解析
7.
某工作的三视图如图所示，现将该工作通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工作的一个面内，则原工件材料的利用率为（）（材料利用率=新工件的体积/原工件的体积）

A、 $\frac{8}{9π}$ B、 $\frac{8}{27 π}$ C、 $\frac{24 (\sqrt{2} - 1)^{2}}{π}$ D、 $\frac{8 (\sqrt{2} - 1)^{2}}{π}$

查看试题解析
8.
执行如图的程序框图，如果输入的x=0，y=1，n=1，则输出x，y的值满足（　　）

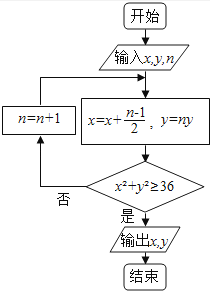A、y=2x B、y=3x C、y=4x D、y=5x

查看试题解析
9. 若将函数y=2sin 2x的图像向左平移 $\frac{π}{12}$ 个单位长度，则评议后图象的对称轴为（）

A、x= $\frac{k π}{2}$ – $\frac{π}{6}$ (k∈Z) B、x= $\frac{k π}{2}$ + $\frac{π}{6}$ (k∈Z) C、x= $\frac{k π}{2}$ – $\frac{π}{12}$ (k∈Z) D、x= $\frac{k π}{2}$ + $\frac{π}{12}$ (k∈Z)

查看试题解析
10. 某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（）

A、588 B、480 C、450 D、120

查看试题解析

二、填空题

11. 把函数 $y = \sin (2 x + \frac{π}{3})$ 的图象向右平移 $\frac{π}{6}$ 个单位，所得到的图象的函数解析式为

查看试题解析
12. 已知实数x ， y满足 ${\begin{cases} x - 2 y + 4 \geq 0 \\ 2 x + y - 2 \geq 0 \\ 3 x - y - 3 \leq 0 \end{cases}$ ，则x²+y²的取值范围是.

查看试题解析
13. 在 $△ A B C$ 中，内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，已知 $△ A B C$ 的面积为 $3 \sqrt{15}$ $b - c = 2 ， \cos A = - \frac{1}{4}$ ，则 $a$ 的值为。

查看试题解析
14. 如图，已知椭圆C的方程为： $\frac{x^{2}}{a} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0），B是它的下顶点，F是其右焦点，BF的延长线与椭圆及其右准线分别交于P、Q两点，若点P恰好是BQ的中点，则此椭圆的离心率是．

查看试题解析

三、综合题

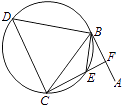
15. 甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得3分；如果只有一个人猜对，则“星队”得1分；如果两人都没猜对，则“星队”得0分．已知甲每轮猜对的概率是 $\frac{3}{4}$ ，乙每轮猜对的概率是 $\frac{2}{3}$ ；每轮活动中甲、乙猜对与否互不影响．各轮结果亦互不影响．假设“星队”参加两轮活动，求：

(1)、“星队”至少猜对3个成语的概率；

(2)、“星队”两轮得分之和为X的分布列和数学期望EX．

查看试题解析
16. 设函数f（x）=x³+ax²+bx+c．

(1)、求曲线y=f（x）在点（0，f（0））处的切线方程；

(2)、设a=b=4，若函数f（x）有三个不同零点，求c的取值范围；

(3)、求证：a²﹣3b＞0是f（x）有三个不同零点的必要而不充分条件．

查看试题解析
17. 如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．

(1)、记平面BEF与平面ABC的交线为l，试判断直线l与平面PAC的位置关系，并加以证明；

(2)、设（1）中的直线l与圆O的另一个交点为D，且点Q满足 $\vec{D Q} = \frac{1}{2} \vec{C P}$ ．记直线PQ与平面ABC所成的角为θ，异面直线PQ与EF所成的角为α，二面角E﹣l﹣C的大小为β．求证：sinθ=sinαsinβ．

查看试题解析
18. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左焦点为F，离心率为 $\frac{\sqrt{3}}{3}$ ，过点F且与x轴垂直的直线被椭圆截得的线段长为 $\frac{4 \sqrt{3}}{3}$ ．

(1)、求椭圆的方程；

(2)、设A，B分别为椭圆的左，右顶点，过点F且斜率为k的直线与椭圆交于C，D两点．若 $\vec{A C} \cdot \vec{D B} + \vec{A D} \cdot \vec{C B}$ =8，求k的值．

查看试题解析
19. 已知数列{a_n}满足a₁=1，a_n+1=3a_n+1．

(1)、证明{a_n+ $\frac{1}{2}$ }是等比数列，并求{a_n}的通项公式；

(2)、证明： $\frac{1}{a_{1}}$ + $\frac{1}{a_{2}}$ +…+ $\frac{1}{a_{n}}$ ＜ $\frac{3}{2}$ ．

查看试题解析

四、选做题

20. 如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D．

(1)、证明：DB=DC；

(2)、设圆的半径为1，BC= $\sqrt{3}$ ，延长CE交AB于点F，求△BCF外接圆的半径．

查看试题解析
21. 已知曲线C： $\frac{x^{2}}{4}$ + $\frac{y^{2}}{9}$ =1，直线l： ${\begin{matrix} x = 2 + t \\ y = 2 - 2 t \end{matrix}$ （t为参数）

(1)、写出曲线C的参数方程，直线l的普通方程．

(2)、过曲线C上任意一点P作与l夹角为30°的直线，交l于点A，求|PA|的最大值与最小值．

查看试题解析
22. 设函数f（x）=|x+ $\frac{1}{a}$ |+|x﹣a|（a＞0）．

(1)、证明：f（x）≥2；

(2)、若f（3）＜5，求a的取值范围．

查看试题解析