2018-2019学年数学北师大版九年级上册第1章 特殊的平行四边形 单元检测b卷
试卷更新日期:2018-09-07 类型:单元试卷
一、选择题
-
1. 如图,正方形ABCD的对角线AC、BD相交于点O,OA=3,则此正方形的面积为( )
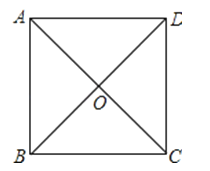 A、3 B、12 C、18 D、362.
A、3 B、12 C、18 D、362.如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形ABDC为( )
 A、菱形 B、正方形 C、矩形 D、一般平行四边形3.
A、菱形 B、正方形 C、矩形 D、一般平行四边形3.如图,要使平行四边形ABCD变为矩形,需要添加的条件是( )
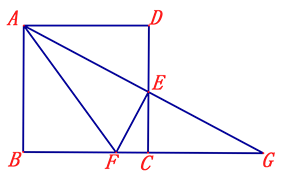
 A、AC=BD B、AD=BC C、AB=CD D、AB=BC4. 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( )
A、AC=BD B、AD=BC C、AB=CD D、AB=BC4. 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( ) A、11 B、16 C、19 D、225. 如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )
A、11 B、16 C、19 D、225. 如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( ) A、45° B、60° C、75° D、90°6. 如图,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且▱ABCD的周长为40,则▱ABCD的面积为( )
A、45° B、60° C、75° D、90°6. 如图,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且▱ABCD的周长为40,则▱ABCD的面积为( ) A、24 B、36 C、40 D、487.
A、24 B、36 C、40 D、487.如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
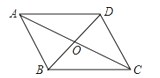 A、18 B、28 C、36 D、468. 如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A、18 B、28 C、36 D、468. 如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( ) A、2 B、4 C、4 D、29. 如图,在 中, 平分 , 于点 , 为 的中点,连接 并延长交 于点E.若 , ,则线段 的长为( ).
A、2 B、4 C、4 D、29. 如图,在 中, 平分 , 于点 , 为 的中点,连接 并延长交 于点E.若 , ,则线段 的长为( ). A、 B、 C、 D、510. 在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:
A、 B、 C、 D、510. 在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:①DN=DM; ② ∠NDM=90°; ③ 四边形CMDN的面积为4; ④△CMN的面积最大为2.
其中正确的结论有( )
 A、①②④; B、①②③; C、②③④; D、①②③④.11. 如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
A、①②④; B、①②③; C、②③④; D、①②③④.11. 如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )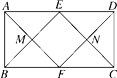 A、正方形 B、菱形 C、矩形 D、无法确定12. 如图,菱形ABCD中,∠B=60°,AB=2.若点P是菱形ABCD内部一点,满足△PBC是等腰三角形,则线段PD的长不可能是( )
A、正方形 B、菱形 C、矩形 D、无法确定12. 如图,菱形ABCD中,∠B=60°,AB=2.若点P是菱形ABCD内部一点,满足△PBC是等腰三角形,则线段PD的长不可能是( ) A、错误!请输入数字。 B、
A、错误!请输入数字。 B、 C、
D、
C、
D、
二、填空题
-
13. 矩形的两条对角线的夹角为600 , 较短的边长为6cm,则对角线的长为cm.14. 如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积为3,那么△PDC与△PAB的面积和等于
 15. 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线长为 .
15. 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线长为 . 16. 如图所示,在▱ABCD中,E,F为对角线BD上的两点,要使四边形AECF为平行四边形,在不连接其他线段的前提下,还需要添加的一个条件是 .
16. 如图所示,在▱ABCD中,E,F为对角线BD上的两点,要使四边形AECF为平行四边形,在不连接其他线段的前提下,还需要添加的一个条件是 .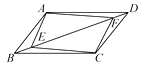 17. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .
17. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .
三、解答题
-
18. 如图,▱ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F,求证:OE=OF.
 19. 如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.
19. 如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值. 20. 如图,在▱ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
20. 如图,在▱ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF. (1)、求证:四边形ABEF是菱形;(2)、连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.21. 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形ABEF是菱形;(2)、连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.21. 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD. (1)、求证:四边形AODE是矩形;(2)、若AB=4,∠BCD=120°,求四边形AODE的面积.22. 如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1)、求证:四边形AODE是矩形;(2)、若AB=4,∠BCD=120°,求四边形AODE的面积.22. 如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E. (1)、求∠ABD的度数;(2)、求线段BE的长.23. 如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)、求∠ABD的度数;(2)、求线段BE的长.23. 如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.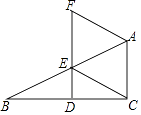 (1)、证明:AF=CE;(2)、当∠B=30°时,试判断四边形ACEF的形状并说明理由.
(1)、证明:AF=CE;(2)、当∠B=30°时,试判断四边形ACEF的形状并说明理由.