河南省鹤壁市2017-2018学年高一下学期数学期末考试试卷

试卷更新日期：2018-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 将 $225 °$ 角化为弧度制为（）

A、 $\frac{3 π}{4}$ B、 $\frac{5 π}{4}$ C、 $\frac{7 π}{4}$ D、 $\frac{9 π}{4}$

查看试题解析
2. 下列抽样实验中，适合用抽签法的有（）

A、从某厂生产的3 000件产品中抽取600件进行质量检验 B、从某厂生产的两箱(每箱15件)产品中取6件进行质量检验 C、从甲、乙两厂生产的两箱(每箱15件)产品中抽取6件进行质量检验 D、从某厂生产的3 000件产品中抽取10件进行质量检验

查看试题解析
3. 已知角 $α$ 的终边经过点 $P (- 5 ， - 12)$ ，则 $sin (\frac{3 π}{2} + α)$ 的值等于（）

A、 $- \frac{5}{13}$ B、 $- \frac{12}{13}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
4. 下列各数中最大的数是（）

A、 $15_{(10)}$ B、 $25_{(6)}$ C、 $100_{(4)}$ D、 $1111_{(2)}$

查看试题解析
5. 已知某8个数据的平均数为5，方差为3，现又加入一个新数据5，此时这9个数的平均数为 $\bar{x}$ ，方差为 $s^{2}$ ，则（）

A、 $\bar{x} = 5$ ， $s^{2} > 3$ B、 $\bar{x} = 5$ ， $s^{2} < 3$ C、 $\bar{x} > 5$ ， $s^{2} < 3$ D、 $\bar{x} > 5$ ， $s^{2} > 3$

查看试题解析
6. 设平面向量 $\overset{⇀}{a} = (1 ， 2)$ ， $\overset{⇀}{b} = (- 2 ， y)$ ，若 $\overset{⇀}{a} ⊥ \overset{⇀}{b}$ ，则 $| \overset{⇀}{a} + \overset{⇀}{b} |$ 等于（）

A、 $\sqrt{5}$ B、 $\sqrt{6}$ C、 $\sqrt{2}$ D、 $\sqrt{10}$

查看试题解析
7. 某种产品的广告费支出 $x$ 与销售额 $y$ （单位：百万元）之间有如下对应数据：
         $x$
2
4
5
6
8
        $y$
30
40
        $t$
50
70
根据上表提供的数据，求出 $y$ 关于 $x$ 的回归直线方程为 $\hat{y} = 6.5 x + 17.5$ ，则 $t$ 的值为（   ）

A、40 B、50 C、60 D、70

查看试题解析
8. 点 $(1 ， \sqrt{3})$ 到直线 $x cos θ + y sin θ = 1$ 的距离为 $f (θ)$ ，则 $f (θ)$ 的最大值是（）

A、3 B、1 C、 $\sqrt{2} - 1$ D、 $\sqrt{2} + 1$

查看试题解析
9. 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出结果n=（）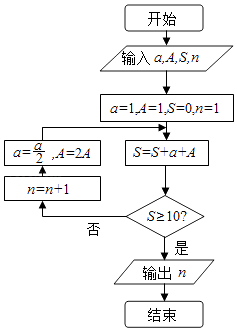

A、4 B、5 C、2 D、3

查看试题解析
10. 如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是（）

A、12.5；12.5 B、13；13 C、13；12.5 D、12.5；13

查看试题解析
11. 已知函数 $f (x) = sin (ω x - \frac{π}{6})$ ， $ω > 0$ 和 $g (x) = 1 - cos (2 x + φ)$ ， $φ \in (- \frac{π}{2} ， \frac{π}{2})$ 的图象的对称轴相同，则 $g (x)$ 在 $[0 ， \frac{π}{2}]$ 上的单调递增区间是（）

A、 $[\frac{π}{3} ， \frac{π}{2}]$ B、 $[0 ， \frac{π}{3}]$ C、 $[\frac{π}{6} ， \frac{π}{3}]$ D、 $[0 ， \frac{π}{6}]$

查看试题解析
12. 如图所示，平面内有三个向量 $\overset{⇀}{O A}$ ， $\overset{⇀}{O B}$ ， $\overset{⇀}{O C}$ . $\overset{⇀}{O A}$ 与 $\overset{⇀}{O B}$ 夹角为 $120 °$ ， $\overset{⇀}{O A}$ 与 $\overset{⇀}{O C}$ 夹角为 $150 °$ ，且 $| \overset{⇀}{O A} | = | \overset{⇀}{O B} | = 1$ ， $| \overset{⇀}{O C} | = 2 \sqrt{3}$ ，若 $\overset{⇀}{O C} = λ \overset{⇀}{O A} + μ \overset{⇀}{O B} (λ ， μ \in R)$ ，则 $λ + μ =$ （）

A、1 B、 $- \frac{9}{2}$ C、-6 D、6

查看试题解析

二、填空题

13. 两个数4830与3289的最大公约数是．

查看试题解析
14. 如图，在 $Δ A B C$ 中， $∠ B A C = 60 °$ ， $A B = 2$ ， $A C = 1$ ， $D$ 是 $B C$ 边上的一点，脯 $\overset{⇀}{C D} = 2 \overset{⇀}{D B}$ ，则 $\overset{⇀}{A D} \cdot \overset{⇀}{B C}$ 的值为．

查看试题解析
15. 在区间 $[- π ， π]$ 内随机取出两个数分别记为 $a$ 、 $b$ ，则函数 $f (x) = x^{2} + 2 a x - b^{2} + π^{2}$ 有零点的概率为．

查看试题解析
16. 已知 $f (x) = sin (φ x + \frac{π}{3}) (φ > 0)$ ， $f (\frac{π}{6}) = f (\frac{π}{3})$ ，且 $f (x)$ 在区间 $(\frac{π}{6} ， \frac{π}{3})$ 只有最小值，没有最大值，则 $φ$ 的值是．

查看试题解析

三、解答题

17. 已知 $\frac{π}{4} < α < \frac{π}{2}$ ， $tan α + \frac{1}{tan α} = \frac{10}{3}$ .

(1)、求 $tan α$ 的值；

(2)、求 $\frac{sin (2 π - α) cos (\frac{π}{2} + α) cos (\frac{11 π}{2} - α)}{sin (3 π - α) sin (- π - α) sin (\frac{9 π}{2} + α)}$ 的值.

查看试题解析
18. 某校高一（1）班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图所示，据此解答如下问题：

(1)、求该班全体男生的人数；

(2)、求分数在 $[80 ， 90)$ 之间的男生人数，并计算频率分布直方图中 $[80 ， 90)$ 之间的矩形的高.

查看试题解析
19. 某实验室白天的温度 $f (t)$ （单位： $° C$ ）随时间 $t$ （单位： $h$ ）的变化近似满足函数关系： $f (t) = 10 - 2 sin (\frac{π}{12} t + \frac{π}{3})$ ， $t \in [6 ， 18]$ .

(1)、求实验室白天的最大温差；

(2)、若要求实验室温差不高于 $11 ° C$ ，则在哪段时间实验室需要降温？

查看试题解析
20. 某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：
日期
12月1日
12月2日
12月3日
12月4日
12月5日
温差 $x (° C)$
10
11
13
12
8
发芽数 $y$ （颗）
23
25
30
26
16
该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验.

(1)、求选取的2组数据恰好是不相邻2天数据的概率；

(2)、若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出 $y$ 关于 $x$ 的线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ ；

(3)、若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？（参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ）

查看试题解析
21. 已知函数 $\overset{⇀}{m} = (sin ω x + cos ω x ， \sqrt{3} cos ω x)$ ， $\overset{⇀}{n} = (cos ω x - sin ω x ， 2 sin ω x) (ω > 0)$ ，函数 $f (x) = \overset{⇀}{m} \cdot \overset{⇀}{n} + t$ ，若 $f (x)$ 的图象上相邻两条对称轴的距离为 $\frac{π}{4}$ ，图象过点 $(0 ， 0)$ .

(1)、求 $f (x)$ 表达式和 $f (x)$ 的单调增区间；

(2)、将函数 $f (x)$ 的图象向右平移 $\frac{π}{8}$ 个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数 $y = g (x)$ 的图象，若函数 $F (x) = g (x) + k$ 在区间 $[0 ， \frac{π}{2}]$ 上有且只有一个零点，求实数 $k$ 的取值范围.

查看试题解析

日期	12月1日	12月2日	12月3日	12月4日	12月5日
温差 $x (° C)$	10	11	13	12	8
发芽数 $y$ （颗）	23	25	30	26	16

$x$	2	4	5	6	8
$y$	30	40	$t$	50	70