2018-2019学年数学人教版（五四学制）九年级上册28.2二次函数与一元二次方程同步练习

试卷更新日期：2018-09-06 类型：同步测试

进入出卷网下载

一、单选题

1. 抛物线y＝－2x²－x＋2与坐标轴的交点个数是（）

A、3 B、2 C、1 D、0

查看试题解析
2. 已知二次函数y=ax²+bx+c，且a＜0，a﹣b+c＞0，则一定有（）

A、b²﹣4ac＞0 B、b²﹣4ac=0 C、b²﹣4ac＜0 D、b²﹣4ac≤0

查看试题解析
3. 下列二次函数的图象与x轴有两个不同的交点的是（）

A、y=x² B、y=x²+4 C、y=3x²﹣2x+5 D、y=3x²+5x﹣1

查看试题解析
4. 已知二次函数y＝x²－3x＋m(m为常数)的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程x²－3x＋m＝0的两实数根是（）

A、x₁＝1，x₂＝－1 B、x₁＝1，x₂＝2 C、x₁＝1，x₂＝0 D、x₁＝1，x₂＝3

查看试题解析
5. 二次函数y=﹣x²+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程﹣x²+mx﹣t=0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（）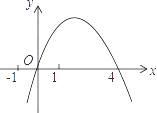

A、t＞﹣5 B、﹣5＜t＜3 C、3＜t≤4 D、﹣5＜t≤4

查看试题解析
6. 根据抛物线y＝x²＋3x－1与x轴的交点的坐标，可以求出下列方程中哪个方程的近似解（）

A、x²＋3x－1＝0 B、x²＋3x＋1＝0 C、3x²＋x－1＝0 D、x²－3x＋1＝（）

查看试题解析
7. 已知抛物线y=ax²+bx+c与x轴交于（x₁ ， 0）、（x₂ ， 0）两点，且0＜x₁＜1，1＜x₂＜5与y轴交于（0，﹣2），下列结论：①2a+b＞1；②a+b＜2；③3a+b＞0；④a＜﹣1，其中正确结论的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，已知二次函数y=ax²+bx+c(a#0)的图象如图所示，给出以下四个结论：
①abc=0，②a+b+c>0，③b=3a， ④4ac—b²<0；其中正确的结论有（）

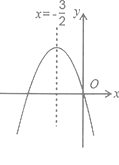A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，已知二次函数y＝x²＋bx＋3的图象与x轴正半轴交于B、C两点，BC＝2，则b的值为（）

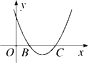A、4 B、－4 C、±4 D、－5

查看试题解析

10. 观察下列表格，一元二次方程x²﹣x﹣1.1=0的最精确的一个近似解是（　　）

x	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
x²﹣x﹣1.1	﹣0.99	﹣0.86	﹣0.71	﹣0.54	﹣0.35	﹣0.14	0.09	0.34	0.61

A、0.09 B、1.1 C、1.6 D、1.7

查看试题解析

二、填空题

11. 若二次函数y=mx²+2x+1的图象与x轴只有一个公共点，则常数m的值是．

查看试题解析
12. 已知关于x的方程x²﹣4x+3﹣a=0在0＜x＜4范围内均有两个根，则a的取值范围是．

查看试题解析
13. $y = a x^{2} + b x + c (a \neq 0)$ 的顶点坐标（-1，-3.2）及部分图象（如图所示），由图象可知关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两个根分别是x₁=1.3和x₂= ．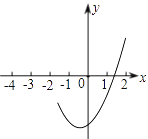

查看试题解析
14. 若关于x的一元二次方程a(x＋m)²－3＝0的两个实数根分别为x₁＝－1，x₂＝3，则抛物线y＝a(x＋m－2)²－3与x轴的交点坐标为．

查看试题解析
15. 已知抛物线y=x²﹣x﹣1与x轴的一个交点的横坐标为m，则代数式m²﹣m+2016的值为．

查看试题解析
16.
如图为二次函数y=ax²+bx+c的图象，根据图象可以得到方程ax²+bx+c=0的一个根在与之间，另一个根在与之间．

查看试题解析

三、解答题

17. 用图象法求下列方程的解：

(1)、x²﹣3x﹣4=0；

(2)、x²﹣6x+2=0（精确到0.1）．

查看试题解析
18.
已知二次函数y=x²﹣4x．
（1）在给出的直角坐标系内用描点法画出该二次函数的图象；
（2）根据所画的函数图象写出当x在什么范围内时，y≤0？
（3）根据所画的函数图象写出方程：x²﹣4x=5的解．

查看试题解析
19. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，根据图象解答下列问题：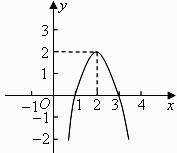

(1)、写出方程 $a x^{2} + b x + c = 0$ 的两个根。

(2)、写出不等式 $a x^{2} + b x + c > 0$ 的解集。

(3)、写出y随x的增大而减小的自变量x的取值范围。

(4)、若方程 $a x^{2} + b x + c = k$ 有两个不相等的实数根，求k的取值范围。

查看试题解析
20. 已知二次函数 $y = x^{2} - m x + m - 2$

(1)、求证：无论m为任何实数，该二次函数的图象与x轴都有两个交点；

(2)、当该二次函数的图象经过点（3，6）时，求此二次函数的解析式.

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，抛物线 $y = m x^{2} - 8 m x + 16 m - 1 (m > 0)$ 与 $x$ 轴的交点分别为 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ ．

(1)、求证：抛物线总与 $x$ 轴有两个不同的交点．

(2)、若 $A B = 2$ ，求此抛物线的解析式．

(3)、已知 $x$ 轴上两点 $C (2 ， 0)$ ， $D (5 ， 0)$ ，若抛物线 $y = m x^{2} - 8 m x + 16 m - 1 (m > 0)$ 与选段 $C D$ 有交点，请写出 $m$ 的取值范围．

查看试题解析
22. 已知：m、n是方程x²﹣6x+5=0的两个实数根，且m＜n，抛物线y=﹣x²+bx+c的图象经过点A（m，0）、B（0，n）．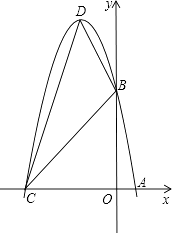

(1)、求这个抛物线的解析式；

(2)、设（1）中抛物线与x轴的另一交点为C，抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；

(3)、P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标．

查看试题解析

2018-2019学年数学人教版（五四学制）九年级上册28.2二次函数与一元二次方程 同步练习

一、单选题

二、填空题

三、解答题

2018-2019学年数学人教版（五四学制）九年级上册28.2二次函数与一元二次方程同步练习