2018-2019学年数学人教版（五四学制）九年级上册28.1二次函数的图象和性质同步练习

试卷更新日期：2018-09-06 类型：同步测试

进入出卷网下载

一、单选题

1. 下列函数不属于二次函数的是（）

A、y=（x﹣1）（x+2） B、y= $\frac{1}{2}$ （x+1）² C、y=1﹣ $\sqrt{3}$ x² D、y=2（x+3）²﹣2x²

查看试题解析
2. 二次函数y=﹣10（x+3）²﹣5的图象的开口方向、对称轴和顶点坐标分别为（）

A、开口向下，对称轴为x=﹣3，顶点坐标为（3，﹣5） B、开口向下，对称轴为x=﹣3，顶点坐标为（﹣3，﹣5） C、开口向上，对称轴为x=3，顶点坐标为（﹣3，5） D、开口向上，对称轴为x=﹣3，顶点坐标为（﹣3，﹣5）

查看试题解析
3. 对于抛物线y=4x﹣4x²+7，有下列说法：①抛物线的开口向上；②顶点坐标为（2，﹣3）；③对称轴为直线x= $\frac{1}{2}$ ；④点（﹣2，﹣17）在抛物线上．其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
4. 在函数 $y = {(x + 1)}^{2} + 3$ 中， $y$ 随 $x$ 增大而减小，则 $x$ 的取值范围为（）

A、 $x$ ＞－1 B、 $x$ ＞3 C、 $x$ ＜－1 D、 $x$ ＜3

查看试题解析
5. 已知二次函数y=﹣3（x﹣h）²+5，当x＞﹣2时，y随x的增大而减小，则有（）

A、h≥﹣2 B、h≤﹣2 C、h＞﹣2 D、h＜﹣2

查看试题解析
6. 下列函数中，当x＞0时，y随x的增大而增大的是（）

A、y=﹣2x+1 B、y=﹣x²﹣1 C、y=（x+1）²﹣1 D、y= $\frac{1}{x}$

查看试题解析
7. 点P₁（﹣1，y₁），P₂（3，y₂），P₃（5，y₃）均在二次函数y=﹣x²+2x+c的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₃＞y₂＞y₁ B、y₃＞y₁=y₂ C、y₁＞y₂＞y₃ D、y₁=y₂＞y₃

查看试题解析
8. 将抛物线y=x²﹣2向左平移1个单位后再向上平移1个单位所得抛物线的表达式为（）

A、 $y = {(x - 1)}^{2} - 1$ B、 $y = {(x + 1)}^{2} - 1$ C、 $y = {(x + 1)}^{2} + 1$ D、 $y = {(x - 1)}^{2} + 1$

查看试题解析
9.
在同一坐标系中，抛物线，，的共同点是（）

A、开口向上，对称轴是y轴，顶点是原点 B、对称轴是y轴，顶点是原点 C、开口向下，对称轴是y轴，顶点是原点 D、有最小值为0

查看试题解析
10. 在下列4个不同的情境中，两个变量所满足的函数关系属于二次函数关系的有（）
①设正方形的边长为x面积为y，则y与x有函数关系；
②x个球队参加比赛，每两个队之间比赛一场，则比赛的场次数y与x之间有函数关系；
③设正方体的棱长为x，表面积为y，则y与x有函数关系；
④若一辆汽车以120km/h的速度匀速行驶，那么汽车行驶的里程y（km）与行驶时间x（h）有函数关系．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 写出一个开口向下，经过点（0，3）的抛物线的表达式．

查看试题解析
12. 已知抛物线y=ax²+bx+c过（﹣1，1）和（5，1）两点，那么该抛物线的对称轴是直线．

查看试题解析
13. 已知y= $\frac{1}{3}$ （x+1）²﹣2，图象的顶点坐标为，当x时，函数值随x的增大而减小．

查看试题解析
14. 在平面直角坐标系中，若将抛物线y=﹣（x+3）²+1先向左平移2个单位长度，再向下平移3个单位长度，则经过这两次平移后所得抛物线的顶点坐标是．

查看试题解析
15. 已知二次函数y=x²+bx+c的图象过点A（1，m），B（3，m），若点M（﹣2，y₁），N（﹣1，y₂），K（8，y₃）也在二次函数y=x²+bx+c的图象上，将y₁ ， y₂ ， y₃按从小到大的顺序用“＜”连接，结果是．

查看试题解析
16. 将抛物线y=ax²+bx+c沿x轴向左平移2个单位，再沿y轴向上平移3个单位，得到的抛物线的函数解析式为y=x²﹣2x+1，则a、b、c分别等于、、．

查看试题解析

三、解答题

17. 已知抛物线过（1，0）、（3，0）、（﹣1，1）三点，求它的函数关系式．

查看试题解析
18. 在同一坐标系中，画出函数y₁＝2x² ， y₂＝2(x－2)²与y₃＝2(x＋2)²的图象，并说明y₂ ， y₃的图象与y₁＝2x²的图象的关系．

查看试题解析
19. 把下列函数化为y=a（x+m）²+k形式，并求出各函数图象的顶点坐标、对称轴、最大值或最小值：

(1)、y=x²﹣2x+4；

(2)、y=100﹣5x² ．

查看试题解析
20. 已知函数y=﹣x²+（m﹣1）x+m（m为常数）．

(1)、求证：不论m为何值，该函数图象的顶点都在函数y=（x+1）²的图象上．

(2)、当﹣2≤m≤3时，求该函数的图象的顶点纵坐标的取值范围．

查看试题解析
21. 如图，二次函数的图象的顶点坐标为（1， $\frac{2}{3}$ ），现将等腰直角三角板直角顶点放在原点O，一个锐角顶点A在此二次函数的图象上，而另一个锐角顶点B在第二象限，且点A的坐标为（2，1）.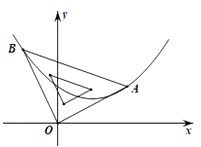

(1)、求该二次函数的表达式；

(2)、判断点B是否在此二次函数的图象上，并说明理由.

查看试题解析
22. 立定跳远时，以小明起跳时重心所在竖直方向为y轴（假设起跳时重心与起跳点在同一竖直方向上），地平线为x轴，建立平面直角坐标系（如图），则小明此跳重心所走过的路径是一条形如y=﹣0.2（x﹣1）²+0.7的抛物线，在最后落地时重心离地面0.3m（假如落地时重心与脚后跟在同一竖直方向上）．

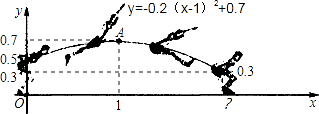(1)、小明在这一跳中，重心离地面最高时距离地面多少米？此时他离起跳点的水平距离有多少米？

(2)、小明此跳在起跳时重心离地面有多高？

(3)、小明这一跳能得满分吗（2.40m为满分）？

查看试题解析

2018-2019学年数学人教版（五四学制）九年级上册28.1二次函数的图象和性质 同步练习

一、单选题

二、填空题

三、解答题

2018-2019学年数学人教版（五四学制）九年级上册28.1二次函数的图象和性质同步练习