云南省曲靖市2018年中考数学试卷
试卷更新日期:2018-09-05 类型:中考真卷
一、选择题
-
1. ﹣2的绝对值是( )A、2 B、-2 C、 D、42. 如图所示的支架(一种小零件)的两个台阶的高度和宽度相等,则它的左视图为( )
 A、
A、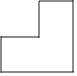 B、
B、 C、
C、 D、
D、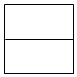 3. 下列计算正确的是( )A、a2•a=a2 B、a6÷a2=a3 C、a2b﹣2ba2=﹣a2b D、(﹣ )3=﹣4. 截止2018年5月末,中国人民银行公布的数据显示,我国外汇的储备规模约为3.11×104亿元美元,则3.11×104亿表示的原数为( )A、2311000亿 B、31100亿 C、3110亿 D、311亿5. 若一个正多边形的内角和为720°,则这个正多边形的每一个内角是( )A、60° B、90° C、108° D、120°6. 下列二次根式中能与2 合并的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,将△OAB(顶点为网格线交点)绕原点O顺时针旋转90°,得到△OA′B′,若反比例函数y= 的图象经过点A的对应点A′,则k的值为( )
3. 下列计算正确的是( )A、a2•a=a2 B、a6÷a2=a3 C、a2b﹣2ba2=﹣a2b D、(﹣ )3=﹣4. 截止2018年5月末,中国人民银行公布的数据显示,我国外汇的储备规模约为3.11×104亿元美元,则3.11×104亿表示的原数为( )A、2311000亿 B、31100亿 C、3110亿 D、311亿5. 若一个正多边形的内角和为720°,则这个正多边形的每一个内角是( )A、60° B、90° C、108° D、120°6. 下列二次根式中能与2 合并的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,将△OAB(顶点为网格线交点)绕原点O顺时针旋转90°,得到△OA′B′,若反比例函数y= 的图象经过点A的对应点A′,则k的值为( )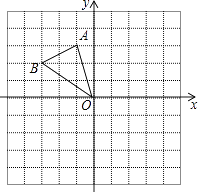 A、-6 B、﹣3 C、3 D、68. 如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB,AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A,E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF= ,④S△CGE:S△CAB=1:4.其中正确的是( )
A、-6 B、﹣3 C、3 D、68. 如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB,AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A,E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF= ,④S△CGE:S△CAB=1:4.其中正确的是( )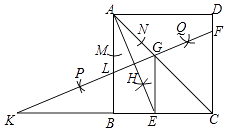 A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
9. 如果水位升高2m时,水位的变化记为+2m,那么水位下降3m时,水位的变化情况应记为 .10. 如图:四边形ABCD内接于⊙O,E为BC延长线上一点,若∠A=n°,则∠DCE=°.
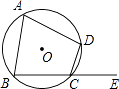 11. 如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是 .
11. 如图:在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是 .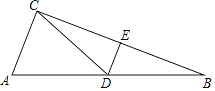 12. 关于x的方程ax2+4x﹣2=0(a≠0)有实数根,那么负整数a=(一个即可).
12. 关于x的方程ax2+4x﹣2=0(a≠0)有实数根,那么负整数a=(一个即可).
13. 一个书包的标价为115元,按8折出售仍可获利15%,该书包的进价为元.14. 如图:图象①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北,正南,西北方向同时平移,每次移动一个单位长度,第一次移动后图形①②③的圆心依次为P1P2P3 , 第二次移动后图形①②③的圆心依次为P4P5P6…,依此规律,P0P2018=个单位长度.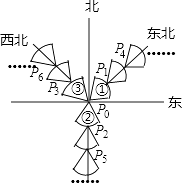
三、解答题
-
15. 计算﹣(﹣2)+(π﹣3.14)0+ +(﹣ )﹣116. 先化简,再求值( ﹣ )÷ ,其中a,b满足a+b﹣ =0.17. 如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.
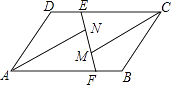 (1)、求证:△AFN≌△CEM;
(1)、求证:△AFN≌△CEM;
(2)、若∠CMF=107°,∠CEM=72°,求∠NAF的度数.18. 甲乙两人做某种机械零件,已知甲每小时比乙多做4个,甲做120个所用的时间与乙做100个所用的时间相等,求甲乙两人每小时各做几个零件?
19. 某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.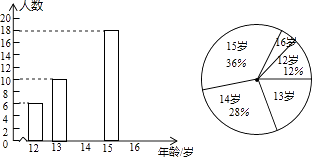
依据以上信息解答以下问题:
(1)、求样本容量;(2)、直接写出样本容量的平均数,众数和中位数;(3)、若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
20. 某公司计划购买A,B两种型号的电脑,已知购买一台A型电脑需0.6万元,购买一台B型电脑需0.4万元,该公司准备投入资金y万元,全部用于购进35台这两种型号的电脑,设购进A型电脑x台.
(1)、求y关于x的函数解析式;
(2)、若购进B型电脑的数量不超过A型电脑数量的2倍,则该公司至少需要投入资金多少万元?
21. 数学课上,李老师准备了四张背面看上去无差别的卡片A,B,C,D,每张卡片的正面标有字母a,b,c表示三条线段(如图),把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.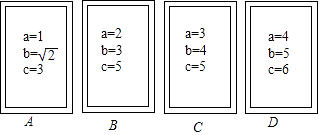 (1)、用树状图或者列表表示所有可能出现的结果;(2)、求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.22. 如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)、用树状图或者列表表示所有可能出现的结果;(2)、求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.22. 如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.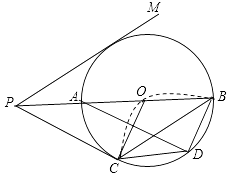 (1)、判断PM与⊙O的位置关系,并说明理由;
(1)、判断PM与⊙O的位置关系,并说明理由;
(2)、若PC= ,求四边形OCDB的面积.23. 如图:在平面直角坐标系中,直线l:y= x﹣ 与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x= .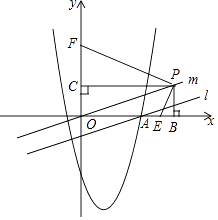 (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PF=3PE.求证:PE⊥PF;(3)、若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.