山西省2018年中考数学试卷

试卷更新日期：2018-09-05 类型：中考真卷

进入出卷网下载

一、选择题

1. 下面有理数比较大小，正确的是（）

A、0＜﹣2 B、﹣5＜3 C、﹣2＜﹣3 D、1＜﹣4

查看试题解析
2. “算经十书”是指汉唐一千多年间的十部著名数学著作，它们曾经是隋唐时期国子监算学科的教科书，这些流传下来的古算书中凝聚着历代数学家的劳动成果．下列四部著作中，不属于我国古代数学著作的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、（﹣a³）²=﹣a⁶ B、2a²+3a²=6a² C、2a²•a³=2a⁶ D、 $（ - \frac{b^{2}}{2 a} ）^{3} = - \frac{b^{6}}{8 a^{3}}$

查看试题解析
4. 下列一元二次方程中，没有实数根的是（）

A、x²﹣2x=0 B、x²+4x﹣1=0 C、2x²﹣4x+3=0 D、3x²=5x﹣2

查看试题解析
5. 近年来快递业发展迅速，下表是2018年1～3月份我省部分地市邮政快递业务量的统计结果（单位：万件）：
太原市
大同市
长治市
晋中市
运城市
临汾市
吕梁市
3303.78
332.68
302.34
319.79
725.86
416.01
338.87
1～3月份我省这七个地市邮政快递业务量的中位数是（）

A、319.79万件 B、332.68万件 C、338.87万件 D、416.01万件

查看试题解析
6. 黄河是中华民族的象征，被誉为母亲河，黄河壶口瀑布位于我省吉县城西45千米处，是黄河上最具气势的自然景观．其落差约30米，年平均流量1010立方米/秒．若以小时作时间单位，则其年平均流量可用科学记数法表示为（）

A、6.06×10⁴立方米/时 B、3.136×10⁶立方米/时 C、3.636×10⁶立方米/时 D、36.36×10⁵立方米/时

查看试题解析
7. 在一个不透明的袋子里装有两个黄球和一个白球，它们除颜色外都相同，随机从中摸出一个球，记下颜色后放回袋子中，充分摇匀后，再随机摸出一个球．两次都摸到黄球的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{1}{3}$ C、 $\frac{2}{9}$ D、 $\frac{1}{9}$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=6，将△ABC绕点C按逆时针方向旋转得到△A'B'C'，此时点A'恰好在AB边上，则点B'与点B之间的距离为（）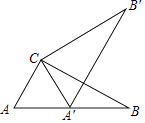

A、12 B、6 C、6 $\sqrt{2}$ D、 $6 \sqrt{3}$

查看试题解析
9. 用配方法将二次函数y=x²﹣8x﹣9化为y=a（x﹣h）²+k的形式为（）

A、y=（x﹣4）²+7 B、y=（x﹣4）²﹣25 C、y=（x+4）²+7 D、y=（x+4）²﹣25

查看试题解析
10. 如图，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，以AC长为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积为（）

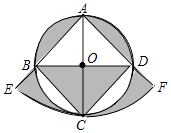A、4π﹣4 B、4π﹣8 C、8π﹣4 D、8π﹣8

查看试题解析

二、填空题

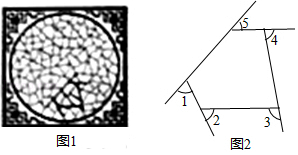
11. 计算：（3 $\sqrt{2}$ +1）（3 $\sqrt{2}$ ﹣1）= ．

查看试题解析
12. 图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消溶，形状无一定规则，代表一种自然和谐美．图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5=度．

查看试题解析
13. 2018年国内航空公司规定：旅客乘机时，免费携带行李箱的长，宽，高三者之和不超过115cm．某厂家生产符合该规定的行李箱．已知行李箱的宽为20cm，长与高的比为8：11，则符合此规定的行李箱的高的最大值为cm．

查看试题解析
14. 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D是AB的中点，以CD为直径作⊙O，⊙O分别与AC，BC交于点E，F，过点F作⊙O的切线FG，交AB于点G，则FG的长为．

查看试题解析

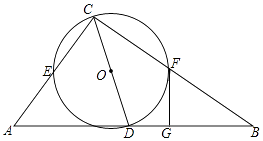
三、解答题

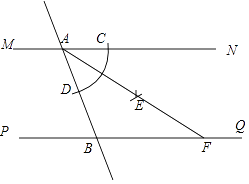
15. 如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B．小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于 $\frac{1}{2}$ CD长为半径作弧，两弧在∠NAB内交于点E；③作射线AE交PQ于点F．若AB=2，∠ABP=60°，则线段AF的长为．

查看试题解析
16. 计算：

(1)、（2 $\sqrt{2}$ ）²﹣|﹣4|+3^﹣¹×6+2⁰；

(2)、 $\frac{x - 2}{x - 1} \cdot \frac{x^{2} - 1}{x^{2} - 4 x + 4} - \frac{1}{x - 2}$ ．

查看试题解析
17. 如图，一次函数y₁=k₁x+b（k₁≠0）的图象分别与x轴，y轴相交于点A，B，与反比例函数y₂= $\frac{k_{2}}{x} (k_{2} \neq 0)$ 的图象相交于点C（﹣4，﹣2），D（2，4）．

(1)、求一次函数和反比例函数的表达式；

(2)、当x为何值时，y₁＞0；

(3)、当x为何值时，y₁＜y₂ ，请直接写出x的取值范围．

查看试题解析
18. 在“优秀传统文化进校园”活动中，学校计划每周二下午第三节课时间开展此项活动，拟开展活动项目为：剪纸，武术，书法，器乐，要求七年级学生人人参加，并且每人只能参加其中一项活动．教务处在该校七年级学生中随机抽取了100名学生进行调查，并对此进行统计，绘制了如图所示的条形统计图和扇形统计图（均不完整）．
请解答下列问题：

(1)、请补全条形统计图和扇形统计图；

(2)、在参加“剪纸”活动项目的学生中，男生所占的百分比是多少？

(3)、若该校七年级学生共有500人，请估计其中参加“书法”项目活动的有多少人？

(4)、学校教务处要从这些被调查的女生中，随机抽取一人了解具体情况，那么正好抽到参加“器乐”活动项目的女生的概率是多少？

查看试题解析

19. 祥云桥位于省城太原南部，该桥塔主体由三根曲线塔柱组合而成，全桥共设13对直线型斜拉索，造型新颖，是“三晋大地”的一种象征．某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动，他们制订了测量方案，并利用课余时间借助该桥斜拉索完成了实地测量．测量结果如下表．

项目	内容
课题	测量斜拉索顶端到桥面的距离
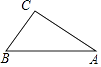
测量示意图		说明：两侧最长斜拉索AC，BC相交于点C，分别与桥面交于A，B两点，且点A，B，C在同一竖直平面内．
测量数据	∠A的度数	∠B的度数	AB的长度
	38°	28°	234米
…	…

(1)、请帮助该小组根据上表中的测量数据，求斜拉索顶端点C到AB的距离（参考数据：sin38°≈0.6，cos38°≈0.8，tan38°≈0.8，sin28°≈0.5，cos28°≈0.9，tan28°≈0.5）

(2)、该小组要写出一份完整的课题活动报告，除上表的项目外，你认为还需要补充哪些项目（写出一个即可）．

查看试题解析

20. 2018年1月20日，山西迎来了“复兴号”列车，与“和谐号”相比，“复兴号”列车时速更快，安全性更好．已知“太原南﹣北京西”全程大约500千米，“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米，其行驶时间是该列“和谐号”列车行驶时间的 $\frac{4}{5}$ （两列车中途停留时间均除外）．经查询，“复兴号”G92次列车从太原南到北京西，中途只有石家庄一站，停留10分钟．求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间．

查看试题解析
21. 请阅读下列材料，并完成相应的任务：
在数学中，利用图形在变化过程中的不变性质，常常可以找到解决问题的办法．著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子：请问如何在一个三角形ABC的AC和BC两边上分别取一点X和Y，使得AX=BY=XY．（如图）解决这个问题的操作步骤如下：
第一步，在CA上作出一点D，使得CD=CB，连接BD．第二步，在CB上取一点Y'，作Y'Z'∥CA，交BD于点Z'，并在AB上取一点A'，使Z'A'=Y'Z'．第三步，过点A作AZ∥A'Z'，交BD于点Z．第四步，过点Z作ZY∥AC，交BC于点Y，再过点Y作YX∥ZA，交AC于点X．
则有AX=BY=XY．
下面是该结论的部分证明：
证明：∵AZ∥A'Z'，∴∠BA'Z'=∠BAZ，
又∵∠A'BZ'=∠ABZ．∴△BA'Z'～△BAZ．
∴ $\frac{Z' A'}{Z A} = \frac{B Z'}{B Z}$ ．
同理可得 $\frac{Z' Y'}{Z Y} = \frac{B Z'}{B Z}$ ．∴ $\frac{Z' A'}{Z A} = \frac{Y' Z'}{Y Z}$ ．
∵Z'A'=Y'Z'，∴ZA=YZ．
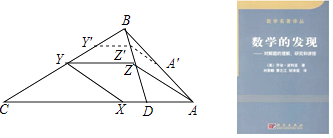
任务：

(1)、请根据上面的操作步骤及部分证明过程，判断四边形AXYZ的形状，并加以证明；

(2)、请再仔细阅读上面的操作步骤，在（1）的基础上完成AX=BY=XY的证明过程；

(3)、上述解决问题的过程中，通过作平行线把四边形BA'Z'Y'放大得到四边形BAZY，从而确定了点Z，Y的位置，这里运用了下面一种图形的变化是．

A、平移 B、旋转 C、轴对称 D、位似

查看试题解析
2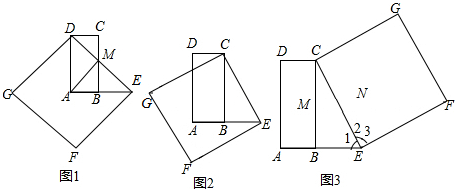2. 综合与实践
问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM．试判断线段AM与DE的位置关系．
探究展示：勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：
证明：∵BE=AB，∴AE=2AB．
∵AD=2AB，∴AD=AE．
∵四边形ABCD是矩形，∴AD∥BC．
∴ $\frac{E M}{D M} = \frac{E B}{A B}$ ．（依据1）
∵BE=AB，∴ $\frac{E M}{D M} = 1$ ．∴EM=DM．
即AM是△ADE的DE边上的中线，
又∵AD=AE，∴AM⊥DE．（依据2）
∴AM垂直平分DE．
反思交流：

(1)、①上述证明过程中的“依据1”“依据2”分别是指什么？
②试判断图1中的点A是否在线段GF的垂直平分线上，请直接回答，不必证明；

(2)、创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明；
探索发现：

(3)、如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C，点B都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．

查看试题解析
23. 综合与探究
如图，抛物线y= $\frac{1}{3} x^{2} - \frac{1}{3} x - 4$ 与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC．点P是第四象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q，过点P作PE∥AC交x轴于点E，交BC于点F．

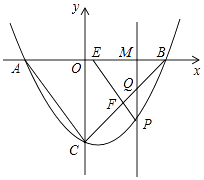(1)、求A，B，C三点的坐标

(2)、试探究在点P运动的过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请直接写出此时点Q的坐标；若不存在，请说明理由；

(3)、请用含m的代数式表示线段QF的长，并求出m为何值时QF有最大值．

查看试题解析

太原市	大同市	长治市	晋中市	运城市	临汾市	吕梁市
3303.78	332.68	302.34	319.79	725.86	416.01	338.87