山东省莱芜市2018年中考数学试卷
试卷更新日期:2018-09-05 类型:中考真卷
一、单选题
-
1. ﹣2的绝对值是( )A、﹣2 B、﹣ C、 D、2
-
2. 经中国旅游研究院综合测算,今年“五一”假日期间全国接待国内游客1.47亿人次,1.47亿用科学记数法表示为( )A、14.7×107 B、1.47×107 C、1.47×108 D、0.147×109
-
3. 无理数2 ﹣3在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间
-
4. 下列图形中,既是中心对称,又是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、
-
5. 若x,y的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、
-
6. 某校举行汉字听写大赛,参赛学生的成绩如下表:
成绩(分)
89
90
92
94
95
人数
4
6
8
5
7
对于这组数据,下列说法错误的是( )
A、平均数是92 B、中位数是92 C、众数是92 D、极差是6 -
7. 已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为( )
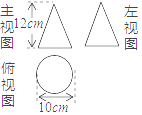 A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm2
A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm2 -
8. 在平面直角坐标系中,已知△ABC为等腰直角三角形,CB=CA=5,点C(0,3),点B在x轴正半轴上,点A在第三象限,且在反比例函数y= 的图象上,则k=( )A、3 B、4 C、6 D、12
-
9. 如图,AB∥CD,∠BED=61°,∠ABE的平分线与∠CDE的平分线交于点F,则∠DFB=( )
 A、149° B、149.5° C、150° D、150.5°
A、149° B、149.5° C、150° D、150.5° -
10. 函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是( )
A、x<﹣4或x>2 B、﹣4<x<2 C、x<0或x>2 D、0<x<2 -
11. 如图,边长为2的正△ABC的边BC在直线l上,两条距离为l的平行直线a和b垂直于直线l,a和b同时向右移动(a的起始位置在B点),速度均为每秒1个单位,运动时间为t(秒),直到b到达C点停止,在a和b向右移动的过程中,记△ABC夹在a和b之间的部分的面积为s,则s关于t的函数图象大致为( )
 A、
A、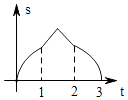 B、
B、 C、
C、 D、
D、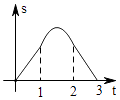
-
12. 如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:①AE=BC②AF=CF③BF2=FG•FC④EG•AE=BG•AB其中正确的个数是( )
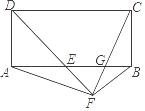 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4
二、填空题
-
13. 计算:(π﹣3.14)0+2cos60°= .
-
14. 已知x1 , x2是方程2x2﹣3x﹣1=0的两根,则x12+x22= .
-
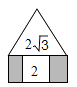
15. 如图,正三角形和矩形具有一条公共边,矩形内有一个正方形,其四个顶点都在矩形的边上,正三角形和正方形的面积分别是2 和2,则图中阴影部分的面积是 .
-
16. 如图,正方形ABCD的边长为2a,E为BC边的中点, 、 的圆心分别在边AB,CD上,这两段圆弧在正方形内交于点F,则E,F间的距离为 .

-
17. 如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA= ,则PB+PC= .

三、解答题
-
18. 先化简,再求值: ,其中a= +1.
-
19. 我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
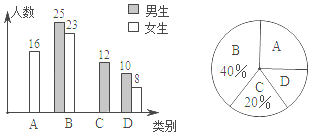 (1)、此次共调查了名学生;
(1)、此次共调查了名学生;
(2)、扇形统计图中D所在扇形的圆心角为;
(3)、将上面的条形统计图补充完整;
(4)、若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
-
20. 在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)
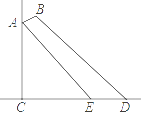
-
21. 已知△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC的中点,将△ADE绕点A按顺时针方向旋转一个角度α(0°<α<90°)得到△AD'E′,连接BD′、CE′,如图1.
 (1)、求证:BD′=CE';
(1)、求证:BD′=CE';
(2)、如图2,当α=60°时,设AB与D′E′交于点F,求 的值. -
22. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)、求甲、乙两种型号的机器人每台的价格各是多少万元;(2)、已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
-
23. 如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
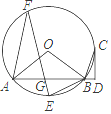 (1)、求证:CD是⊙O的切线;(2)、E为弧AB的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE= ,BE=BG,EG=3 ,求⊙O的半径.
(1)、求证:CD是⊙O的切线;(2)、E为弧AB的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE= ,BE=BG,EG=3 ,求⊙O的半径. -
24. 如图,抛物线y=ax2+bx+c经过A(﹣1,0),B(4,0),C(0,3)三点,D为直线BC上方抛物线上一动点,DE⊥BC于E.
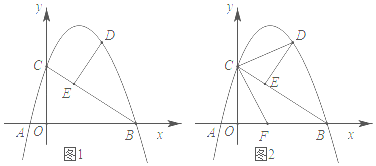 (1)、求抛物线的函数表达式;
(1)、求抛物线的函数表达式;
(2)、如图1,求线段DE长度的最大值;(3)、如图2,设AB的中点为F,连接CD,CF,是否存在点D,使得△CDE中有一个角与∠CFO相等?若存在,求点D的横坐标;若不存在,请说明理由.
