广西壮族自治区梧州市2018年中考数学试卷

试卷更新日期：2018-09-05 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣8的相反数是（）

A、﹣8 B、8 C、- $\frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
2. 研究发现，银原子的半径约是 0.00015 微米，把 0.00015 这个数字用科学记数法表示应是（）

A、1.5×10^﹣⁴ B、1.5×10^﹣⁵ C、15×10^﹣⁵ D、15×10^﹣⁶

查看试题解析
3. 如图，已知 BG 是∠ABC 的平分线，DE⊥AB 于点 E，DF⊥BC 于点 F，DE=6，则 DF 的长度是（）

A、2 B、3 C、4 D、6

查看试题解析
4. 已知∠A=55°，则它的余角是（）

A、25° B、35° C、45° D、55°

查看试题解析
5. 下列各式计算正确的是（）

A、a+2a=3a B、x⁴•x³=x¹² C、（ $\frac{1}{x}$ ）^﹣¹=﹣ $\frac{1}{x}$ D、（x²）³=x⁵

查看试题解析
6. 如图，在正方形 ABCD 中，A，B，C 三点的坐标分别是（﹣1，2）、（﹣1，0）、（﹣3，0），将正方形 ABCD 向右平移 3 个单位，则平移后点 D 的坐标是（）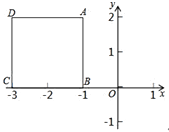

A、（﹣6，2） B、（0，2） C、（2，0） D、（2，2）

查看试题解析
7. 如图，在△ABC 中，AB=AC，∠C=70°，△AB′C′与△ABC 关于直线 EF对称，∠CAF=10°，连接 BB′，则∠ABB′的度数是（）

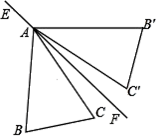A、30° B、35° C、40° D、45°

查看试题解析
8. 一组数据：3，4，5，x，8 的众数是 5，则这组数据的方差是（）

A、2 B、2.4 C、2.8 D、3

查看试题解析
9. 小燕一家三口在商场参加抽奖活动，每人只有一次抽奖机会：在一个不透明的箱子中装有红、黄、白三种球各 1 个，这些球除颜色外无其他差别，从箱子中随机摸出 1 个球，然后放回箱子中轮到下一个人摸球，三人摸到球的颜色都不相同的概率是（）

A、 $\frac{1}{27}$ B、 $\frac{1}{3}$ C、 $\frac{1}{9}$ D、 $\frac{2}{9}$

查看试题解析
10. 九年级一班同学根据兴趣分成 A，B，C，D，E 五个小组，把各小组人数分布绘制成如图所示的不完整统计图．则 D 小组的人数是（）

A、10 人 B、l1 人 C、12 人 D、15 人

查看试题解析
11. 如图，AG：GD=4：1，BD：DC=2：3，则 AE：EC 的值是（）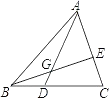

A、3：2 B、4：3 C、6：5 D、8：5

查看试题解析
12. 按一定规律排列的一列数依次为：2，3，10，15，26，35，…，按此规律排列下去，则这列数中的第 100 个数是（）

A、9999 B、10000 C、10001 D、10002

查看试题解析

二、填空题

13. 式子 $\sqrt{x - 3}$ 在实数范围内有意义，则 x 的取值范围是．

查看试题解析
14. 如图，已知在△ABC 中，D、E 分别是 AB、AC 的中点，BC=6cm，则DE 的长度是 cm．

查看试题解析
15. 已知直线 y=ax（a≠0）与反比例函数 y= $\frac{k}{x}$ （k≠0）的图象一个交点坐标为（2，4），则它们另一个交点的坐标是．

查看试题解析
16. 如图，已知在⊙O 中，半径 OA= $\sqrt{2}$ ，弦 AB=2，∠BAD=18°，OD 与AB 交于点 C，则∠ACO= 度．

查看试题解析
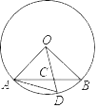17. 如图，圆锥侧面展开得到扇形，此扇形半径 CA=6，圆心角∠ACB=120°，则此圆锥高 OC 的长度是．

查看试题解析
18. 如图，点 C 为 Rt△ACB 与 Rt△DCE 的公共点，∠ACB=∠DCE=90°，连接 AD、BE，过点 C 作 CF⊥AD 于点 F，延长 FC 交 BE 于点 G．若 AC=BC=25，CE=15， DC=20，则 $\frac{E G}{B G}$ 的值为．

查看试题解析

三、解答题

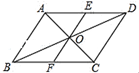
19. 计算： $\sqrt{9}$ ﹣2⁵÷2³+|﹣1|×5﹣（π﹣3.14）⁰

查看试题解析
20. 解方程：2x²﹣x﹣3=0．

查看试题解析
21. 如图，在▱ABCD 中，对角线 AC，BD 相交于点 O，过点 O 的一条直线分别交 AD，BC 于点 E，F．求证：AE=CF．

查看试题解析
22. 解不等式组 ${\begin{matrix} 3 x - 6 \leq x \\ \frac{4 x + 5}{10} < \frac{x + 1}{2} \end{matrix}$ ，并求出它的整数解，再化简代数式 $\frac{x + 3}{x^{2} - 2 x + 1}$ •（ $\frac{x}{x + 3}$ ﹣ $\frac{x - 3}{x^{2} - 9}$ ），从上述整数解中选择一个合适的数，求此代数式的值．

查看试题解析
23. 随着人们生活水平的不断提高，旅游已成为人们的一种生活时尚．为开发新的旅游项目，我市对某山区进行调查，发现一瀑布．为测量它的高度，测量人员在瀑布的对面山上 D 点处测得瀑布顶端 A 点的仰角是 30°，测得瀑布底端 B 点的俯角是 10°，AB与水平面垂直．又在瀑布下的水平面测得 CG=27m， GF=17.6m（注：C、G、F 三点在同一直线上，CF⊥AB 于点 F）．斜坡 CD=20m，坡角∠ECD=40°．求瀑布 AB 的高度．（参考数据： $\sqrt{3}$ ≈1.73，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin10°≈0.17，cos10°≈0.98，tan10°≈0.18）

查看试题解析
24. 我市从 2018 年 1 月 1 日开始，禁止燃油助力车上路，于是电动自行车的市场需求量日渐增多．某商店计划最多投入 8 万元购进 A、B 两种型号的电动自行车共 30 辆，其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元．用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一样．

(1)、求 A、B 两种型号电动自行车的进货单价；

(2)、若 A 型电动自行车每辆售价为 2800 元，B 型电动自行车每辆售价为 3500 元，设该商店计划购进 A 型电动自行车 m 辆，两种型号的电动自行车全部销售后可获利润 y 元．写出 y 与 m 之间的函数关系式；

(3)、该商店如何进货才能获得最大利润？此时最大利润是多少元？

查看试题解析
25. 如图，AB 是⊙M 的直径，BC 是⊙M 的切线，切点为 B，C 是 BC 上（除 B 点外）的任意一点，连接 CM 交⊙M 于点 G，过点 C 作 DC⊥BC 交 BG 的延长线于点 D，连接 AG 并延长交 BC 于点 E．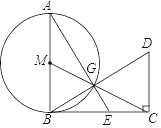

(1)、求证：△ABE∽△BCD；

(2)、若 MB=BE=1，求 CD 的长度．

查看试题解析
26. 如图，抛物线 y=ax2+bx﹣ $\frac{9}{2}$ 与 x 轴交于 A（1，0）、B（6，0）两点，D 是 y 轴上一点，连接 DA，延长 DA 交抛物线于点 E．

(1)、求此抛物线的解析式；

(2)、若 E 点在第一象限，过点 E 作 EF⊥x 轴于点 F，△ADO 与△AEF 的面积比为 $\frac{S_{Δ A D O}}{S_{Δ A E F}}$ = $\frac{1}{9}$ ，求出点 E 的坐标；

(3)、若 D 是 y 轴上的动点，过 D 点作与 x 轴平行的直线交抛物线于 M、N 两点，是否存在点 D，使 DA²=DM•DN？若存在，请求出点 D 的坐标；若不存在，请说明理由．

查看试题解析