2018-2019学年数学沪科版九年级上册21.4 二次函数的应用（1） 同步练习
试卷更新日期：2018-09-05 类型：同步测试
一、选择题
-
1.
如图，在宽为20米，长为32米的矩形地面上修筑同样宽的道路（图中阴影部分），余下部分种植草坪，要使草坪的面积为540平方米，设道路的宽为x米，则下列方程正确的是（ ）
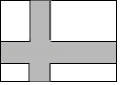A、32×20﹣20x﹣30x=540 B、32×20﹣20x﹣30x﹣x2=540 C、（32﹣x）（20﹣x）=540 D、32×20﹣20x﹣30x+2x2=5402. 如图，从某建筑物10m高的窗口A处用水管向外喷水，喷出的水成抛物线状（抛物线所在平面与墙面垂直）．如果抛物线的最高点M离墙1m，离地面 m，则水流落地点B离墙的距离OB是（ ）
A、2m B、3m C、4m D、5m3. 用长为6m的铝合金型材做一个形状如图所示的矩形窗框，要使做成的窗框的透光面积最大，则该窗的长，宽应分别做成（ ）
A、1.5m，1m B、1m，0.5m C、2m，1m D、2m，0.5m4. 半径是3的圆，如果半径增加2x，那么面积S和x之间的函数关系式是（ ）A、S＝2π（x＋3）2 B、S＝9π＋x C、S＝4πx2＋12x＋9 D、S＝4πx2＋12πx＋9π5. 如图，在平面直角坐标系中，抛物线y= x2经过平移得到抛物线y=ax2+bx，其对称轴与两段抛物线所围成的阴影部分的面积为 ，则a、b的值分别为（ ）
A、 ， B、 ，﹣ C、 ，﹣ D、﹣ ，6.设计师以y=2x2﹣4x+8的图形为灵感设计杯子如图所示，若AB=4，DE=3，则杯子的高CE=（ ）
A、17 B、11 C、8 D、77. 将抛物线 向右平移2个单位，再向下平移1个单位，得到抛物线 ， 与 轴交于 、 两点， 的顶点记为 ，则 的面积为（ ）．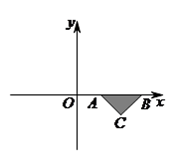
A、1 B、2 C、3 D、48. 如图，在 中， ， ， ．动点P从点A开始沿边AB向点B以 的速度移动，动点 从点 开始沿边 向点 以 的速度移动．若 ， 两点分别从 ， 两点同时出发，在运动过程中， 的最大面积是（ ）．
A、18 B、12 C、9 D、39. 一个长方形的周长为8cm，一边长是xcm，则这个长方形的面积y与边长x的函数关系用图象表示大致为（ ）A、
B、
C、
D、
10. 如图，⊙O的半径为2，C1是函数y＝ x2的图象，C2是函数y＝－ x2的图象，则图中阴影部分的面积为（ ）
A、π B、2π C、3π D、4π二、填空题
-
11. 把20cm长的铁丝剪成两段后，分别围成正方形，则两个正方形面积之和的最小值是 ．12. 学校组织“美丽校园我设计”活动．某同学打算利用学校文化墙的墙角建一个矩形植物园．其中矩形植物园的两邻边之和为4m，设矩形的一边长为 m，矩形的面积为 m2 ． 则函数 的表达式为 ， 该矩形植物园的最大面积是 m2 ．
13. 如图，有长为24米的篱笆，一边利用墙（墙的最大可用长度为3米），围成一个由两个长方形组成的花圃，当花圃的边AB为 米时，围成的花圃面积最大，最大面积为平方米．
14. 抛物线过点A（﹣1，0），B（0，﹣2），C（1，﹣2），且与x轴的另一交点为E，顶点为D，则四边形ABDE的面积为 ．15. 二次函数y== 的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y= 的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积为.
16. 如图，在平面直角坐标系中，抛物线y=﹣x2+4x与x轴交于点A，点M是x轴上方抛物线上一点，过点M作MP⊥x轴于点P，以MP为对角线作矩形MNPQ，连结NQ，则对角线NQ的最大值为 ．
17. 如图，抛物线过点 A(2，0)、B(6，0)、C(1， )，平行于x轴的直线CD交抛物线于C、D，以AB为直径的圆交直线CD于点E、F，则CE+FD的值是 ．
三、解答题
-
18. 如图，用20m的篱笆围成一个矩形的花圃．设连墙的一边为x（m），矩形的面积为y（m2）．
(1)、写出y关于x的函数解析式；(2)、当x=3时，矩形的面积为多少？19. 某景区内有一块矩形油菜花田地（数据如图示，单位：m.）现在其中修建一条观花道（图中阴影部分）供游人赏花.设改造后剩余油菜花地所占面积为ym2.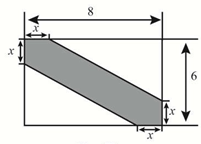
(1)、求y与x的函数表达式；(2)、若改造后观花道的面积为13m2 ， 求x的值；
(3)、若要求 0.5≤ x ≤1，求改造后剩余油菜花地所占面积的最大值.20. 已知矩形的一边长为x，且相邻两边长的和为10．(1)、求矩形面积S与边长x的函数关系式，并写出自变量的取值范围；(2)、求矩形面积S的最大值．21. 在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．
(1)、当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；(2)、当EH：EF＝7：2，且侧面积与底面积之比为9：7时，求x的值．
22. 如图，已知抛物线y＝ax2＋bx＋c经过点A(－1，0)，点B(3，0)和点C(0，3)．
(1)、求抛物线的解析式和顶点E的坐标；(2)、点C是否在以BE为直径的圆上?请说明理由；(3)、点Q是抛物线对称轴上一动点，点R是抛物线上一动点，是否存在点Q、R，使以Q、R、C、B为顶点的四边形是平行四边形?若存在，直接写出点Q、R的坐标，若不存在，请说明理由．23. 已知：如图所示，在△ABC中，∠B=90°，AB=5cm，BC=7cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)、如果P，Q分别从A，B同时出发，那么几秒后，△PBQ的面积等于4cm2？
(2)、如果P，Q分别从A，B同时出发，那么几秒后，△PBQ中PQ的长度等于5cm？
(3)、在（1）中，当P，Q出发几秒时，△PBQ有最大面积?