2018-2019学年数学沪科版九年级上册21.3 二次函数与一元二次方程 同步练习
试卷更新日期：2018-09-05 类型：同步测试
一、选择题
-
1. 函数y＝ax2＋1的图像经过点（－2，0），则 的方程 的实数根为（ ）A、 ， B、 ， C、 ， D、 ，2. 若抛物线y=x2﹣2x﹣1与x轴的交点坐标为（a，0），则代数式a2﹣2a+2017的值为（ ）A、2019 B、2018 C、2017 D、20163. 二次函数y＝ax2＋bx＋c中，函数y与自变量x的部分对应值如下表，则方程ax2＋bx＋c＝0的一个解的范围是（ ）
x
6.17
6.18
6.19
y
－0.03
－0.01
0.02
A、－0.03＜x＜－0.01 B、－0.01＜x＜0.02 C、6.18＜x＜6.19 D、6.17＜x＜6.184. 二次函数y=x2+2x﹣m2+1的图像与直线y=1的公共点个数是（ ）A、0 B、1 C、2 D、1或25. 根据下表，确定方程ax2+bx+c=0的一个解的取值范围是（ ）x
2
2.23
2.24
2.25
ax2+bx+c
﹣0.05
﹣0.02
0.03
0.07
A、2＜x＜2.23 B、2.23＜x＜2.24 C、2.24＜x＜2.25 D、2.24＜x≤2.256. 抛物线y=2（x+1）2﹣2与y轴的交点的坐标是（ ）
A、（0，﹣2） B、（﹣2，0） C、（0，﹣1） D、（0，0）7. 二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=-1，有以下结论：①abc>0；②4ac<b2；③2a+b=0；④a-b+c>2．其中正确的结论的个数是（ ）
A、1 B、2 C、3 D、48. 二次函数 的图象如图，若一元二次方程 有实数解，则k的最小值为（ ）
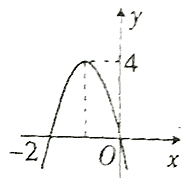A、-4 B、-6 C、-8 D、09. 如图，一段抛物线：y=﹣x（x﹣5）（0≤x≤5），记为C1 ， 它与x轴交于点O，A1；将C1绕点A1旋转180°得C2 ， 交x轴于点A2；将C2绕点A2旋转180°得C3 ， 交x轴于点A3；…如此进行下去，得到一“波浪线”，若点P（2018，m）在此“波浪线”上，则m的值为（ ）
A、4 B、﹣4 C、﹣6 D、610. 已知二次函数y＝x2－5x＋m 的图像与 轴有两个交点，若其中一个交点的坐标为（1，0），则另一个交点的坐标为（ ）A、（－1，0） B、（4，0） C、（5，0） D、（－6，0）二、填空题
-
11. 抛物线y＝2(x＋3)(x－2)与x轴的交点坐标分别为 ．
12. 二次函数 的图象如图，若一元二次方程ax2+bx+m=0有实数根，则
的最大值为 ． 
13. 抛物线y=（2x﹣1）2+t与x轴的两个交点之间的距离为4，则t的值是 ．14. 二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx=m有实数根，则m的最小值为 ．
15. 如图，在平面直角坐标系中，抛物线y= x2﹣x与x轴交于点A，点P在抛物线上，连结AP．若△OAP是以OA为底边的等腰三角形，则△OAP的面积是 ．
16. 已知抛物线 交x轴于点A，B (B在x轴正半轴上），交y轴于点C，△ABC是等腰三角形，则a的值为 ．三、解答题
-
17. 抛物线y=-x2+bx+c过点（0，-3）和（2，1），试确定抛物线的解析式，并求出抛物线与x轴的交点坐标．18. 已知在平面直角坐标系内，抛物线y=x2+bx+6经过x轴上两点A， B，点B的坐标为（3，0），与y轴相交于点C；(1)、求抛物线的表达式；(2)、求△ABC的面积．19. 使得函数值为0的自变量的值称为函数的零点．例如，对于函数y=x﹣1，令y=0可得x=1，我们说1是函数y=x﹣1的零点．已知函数y=x2﹣2mx﹣2（m+3）（m为常数）
(1)、当m=0时，求该函数的零点．(2)、证明：无论m取何值，该函数总有两个零点．20. 已知关于x的一元二次方程 有两个不相等的实数根．(1)、求k的取值范围；(2)、若k取小于1的整数，且此方程的解为整数，则求出此方程的两个整数根；(3)、在（2）的条件下，二次函数 与x轴交于A、B两点（A点在B点的左侧），D点在此抛物线的对称轴上，若∠DAB=60º，直接写出D点的坐标．21. 已知关于x的一元二次方程x2+（k﹣5）x+1﹣k=0（其中k为常数）.(1)、求证无论k为何值，方程总有两个不相等实数根；(2)、已知函数y=x2+（k﹣5）x+1﹣k的图象不经过第三象限，求k的取值范围；(3)、若原方程的一个根大于3，另一个根小于3，求k的最大整数值.