2018-2019学年数学湘教版九年级上册2.5 一元二次方程的应用(2) 同步练习
试卷更新日期:2018-09-03 类型:同步测试
一、选择题
-
1. 我国南宋数学家杨辉曾提出这样一个问题:"直田积(矩形面积),八百六十四(平方步),只云阔(宽)不及长一十二步(宽比长少12步),问阔及长各几步."如果设矩形田地的长为x步,那么同学们列出的下列方程中正确的是 ( )
A、 B、 C、 D、2. 从正方形铁片上截去 宽的一个矩形,剩余矩形的面积为 ,则原来正方形的面积为( ).
A、 B、 C、 D、3. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 .若设道路的宽为 ,则下面所列方程正确的是( )
,则下面所列方程正确的是( ) A、(32-x)(20-x)=32×20-570 B、32x+2×20x=32×20-570 C、32x+2×20x-2x2=570 D、(32-2x)(20-x)= 5704. 如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm,由题意可列方程( )
A、(32-x)(20-x)=32×20-570 B、32x+2×20x=32×20-570 C、32x+2×20x-2x2=570 D、(32-2x)(20-x)= 5704. 如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm,由题意可列方程( ) A、2x·x=24 B、(10-2x)(8-x)=24 C、(10-x)(8-2x)=24 D、(10-2x)(8-x)=485.
A、2x·x=24 B、(10-2x)(8-x)=24 C、(10-x)(8-2x)=24 D、(10-2x)(8-x)=485.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2 , 求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
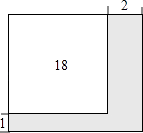 A、(x+1)(x+2)=18 B、x2﹣3x+16=0 C、(x﹣1)(x﹣2)=18 D、x2+3x+16=06. 三角形两边的长分别是8和6,第三边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是( )
A、(x+1)(x+2)=18 B、x2﹣3x+16=0 C、(x﹣1)(x﹣2)=18 D、x2+3x+16=06. 三角形两边的长分别是8和6,第三边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是( )
A、24 B、24或8 C、48 D、87. 将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm 3 ,则原铁皮的边长为( )
A、10cm B、13cm C、14cm D、16cm8. 如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n,…,请你探究出前n行的点数和所满足的规律.若前n行点数和为930,则n=( )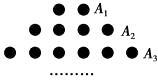
A、29 B、30 C、31 D、32二、填空题
-
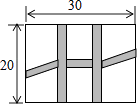
9. 如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2 , 那么小道进出口的宽度应为米.
 10. 如图,点A的坐标为(﹣4,0),直线y= x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为 .
10. 如图,点A的坐标为(﹣4,0),直线y= x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为 . 11. 如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为 .
11. 如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为 . 12. 如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 .
12. 如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 . 13. 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是
13. 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是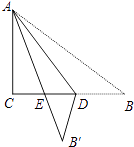 14. 如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形,若 = ,则正△ABC的边长是 .
14. 如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形,若 = ,则正△ABC的边长是 .
三、解答题
-
15. 某小区在绿化工程中有一块长为20m、宽为8m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为56m2 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
 16. 如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
16. 如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米? 17. 李明准备进行如下操作实验,把一根长40cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
17. 李明准备进行如下操作实验,把一根长40cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)、要使这两个正方形的面积之和等于58cm2 , 李明应该怎么剪这根铁丝?
(2)、李明认为这两个正方形的面积之和不可能等于48cm2 , 你认为他的说法正确吗?请说明理由.18. 如图,某农场有一块长40 m,宽32 m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路.要使种植面积为1140 m2 , 求小路的宽. 19. 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的 .
19. 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的 . (1)、求配色条纹的宽度;
(1)、求配色条纹的宽度;
(2)、如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
20. 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图. (1)、当x≥50时,求y关于x的函数关系式;
(1)、当x≥50时,求y关于x的函数关系式;
(2)、若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量;
(3)、为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收 元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
21. 如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发, (1)、如果P、Q同时出发,几秒后,可使△PBQ的面积为8平方厘米?
(1)、如果P、Q同时出发,几秒后,可使△PBQ的面积为8平方厘米?
(2)、线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.