2018-2019学年数学湘教版九年级上册2.1 一元二次方程 同步练习
试卷更新日期：2018-09-03 类型：同步测试
一、选择题
-
1. 若方程（m﹣3）xn+2x﹣3=0是关于x的一元二次方程，则（ ）
A、m=3，n≠2 B、m=3，n=2 C、m≠3，n=2 D、m≠3，n≠22. 下列说法正确的是（ ）A、方程ax2+bx+c=0是关于x的一元二次方程 B、方程3x2=4的常数项是4 C、若一元二次方程的常数项为0，则0必是它的一个根 D、当一次项系数为0时，一元二次方程总有非零解3. 若x=﹣2是关于x的一元二次方程x2+ ax﹣a2=0的一个根，则a的值为（ ）A、﹣1或4 B、﹣1或﹣4 C、1或﹣4 D、1或44. 下列方程中，一元二次方程共有（ ）个①x2﹣2x﹣1=0；②ax2+bx+c=0；③+3x﹣5=0；④﹣x2=0；⑤（x﹣1）2+y2=2；⑥（x﹣1）（x﹣3）=x2 ．
A、1 B、2 C、3 D、45. 一元二次方程2x2﹣5x﹣4=0的二次项系数、一次项系数及常数项分别是（ ）
A、2，5，﹣4 B、2，5，4 C、2，﹣5，﹣4 D、2，﹣5，46. 若关于x的方程x2+（m+1）x+ =0的一个实数根的倒数恰是它本身，则m的值是（ ）A、﹣ B、 C、﹣ 或 D、17. 若ax2﹣5x+3=0是一元二次方程，则不等式3a+6＞0的解集是（ ）
A、a＞﹣2 B、a＞﹣2且a≠0 C、a D、a＜﹣28. 欧几里得的《原本》记载，形如x2＋ax=b2的方程的图解法是；画Rt△ABC，使∠ACB=90°，BC= ，AC=b，再在斜边AB上截取BD= 。则该方程的一个正根是（ ）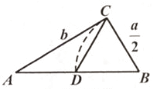
A、AC的长 B、AD的长 C、BC的长 D、CD的长9. 现有一块长方形绿地，它的短边长为20 m，若将短边增大到与长边相等(长边不变)，使扩大后的绿地的形状是正方形，则扩大后的绿地面积比原来增加300 m2 ， 设扩大后的正方形绿地边长为xm，下面所列方程正确的是（ ）
A、x(x-20)=300 B、x(x+20)=300 C、60(x+20)=300 D、60(x-20)=300二、填空题
-
10. 已知（m﹣1）x|m|+1﹣3x+1=0是关于x的一元二次方程，则m= ．
11. 方程2(x＋2)＋8＝3x(x－1)的一般形式为 ， 二次项系数是 ， 一次项系数是 ， 常数项是 ．
12. 已知关于x的一元二次方程2x2﹣3mx﹣5=0的一个根是﹣1，则m= ．13. 若一元二次方程（a≠0） 有一个根为1，则 ；若有一个根是-1，则b与 、c之间的关系为；若有一个根为0，则c=.
14. 当c=时，关于x的方程x2+8x+c=0有一根为0．
15. 当m时，方程（m－1）x2－(2m－1)x＋m＝0是关于x的一元一次方程；当m时，上述方程才是关于x的一元二次方程.
16. 关于x的方程a（x+m）2+b=0的解是x1=2，x2=﹣1，（a，b，m均为常数，a≠0），则方程a（x+m+2）2+b=0的解是 ．
17. 已知m是关于x的方程x2﹣2x﹣7=0的一个根，则2（m2﹣2m）= ．
18. 一次会议上，每两个参加会议的人都相互握一次手，有人统计一共握了36次手，设到会的人数为x人，则根据题意列方程为 ．
三、解答题
-
19. 已知m是一元二次方程x2﹣3x﹣2=0的实数根，求代数式 的值．20. 先化简，再求值： ÷（m+2﹣ ）．其中m是方程x2+3x﹣1=0的根．
21. 有这样的题目：把方程 x2－x＝2化为一元二次方程的一般形式，并写出它的二次项系数，一次项系数和常数项．现在把上面的题目改编成下面的两个小题，请回答问题：
(1)、下面式子中是方程 x2－x＝2化为一元二次方程的一般形式的是 ． (只填写序号)① x2－x－2＝0，②－ x2＋x＋2＝0，③x2－2x＝4，④－x2＋2x＋4＝0，⑤ x2－2 x－4 ＝0.
(2)、方程 x2－x＝2化为一元二次方程的一般形式后，它的二次项系数，一次项系数和常数项之间具有什么关系？