2018-2019学年数学华师大版九年级上册22.2.4 一元二次方程根的判别式 同步练习
试卷更新日期:2018-09-03 类型:同步测试
一、选择题
-
1. 下列方程中,没有实数根的是( )A、x2﹣4x+4=0 B、x2﹣2x+5=0 C、x2﹣2x=0 D、x2﹣2x﹣3=02. 已知关于x的一元二次方程3x2+4x﹣5=0,下列说法正确的是( )A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、没有实数根 D、无法确定3. 若关于x的一元二次方程4x2﹣4x+c=0有两个相等实数根,则c的值是( )A、﹣1 B、1 C、﹣4 D、44. 若关于x的方程x2+x﹣a+ =0有两个不相等的实数根,则实数a的取值范围是( )A、a≥2 B、a≤2 C、a>2 D、a<25. 若关于x的一元二次方程kx2﹣4x+3=0有实数根,则k的非负整数值是( )A、1 B、0,1 C、1,2 D、1,2,36. 判断一元二次方程式x2﹣8x﹣a=0中的a为下列哪一个数时,可使得此方程式的两根均为整数?( )A、12 B、16 C、20 D、247. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、
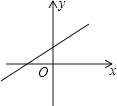 B、
B、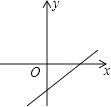 C、
C、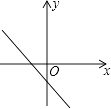 D、
D、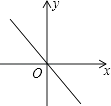 8. 若a满足不等式组 ,则关于x的方程(a﹣2)x2﹣(2a﹣1)x+a+ =0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、以上三种情况都有可能
8. 若a满足不等式组 ,则关于x的方程(a﹣2)x2﹣(2a﹣1)x+a+ =0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、以上三种情况都有可能二、填空题
-
9. 关于x的方程kx2﹣4x﹣ =0有实数根,则k的取值范围是 .10. 若一元二次方程(m﹣1)x2﹣4x﹣5=0没有实数根,则m的取值范围是 .11. 关于x的方程mx2+x﹣m+1=0,有以下三个结论:①当m=0时,方程只有一个实数解;②当m≠0时,方程有两个不等的实数解;③无论m取何值,方程都有一个负数解,其中正确的是(填序号).12. 关于x的方程kx2﹣4x﹣4=0有两个不相等的实数根,则k的最小整数值为 .13. 等腰三角形三边长分别为 ,且 是关于 的一元二次方程 的两根,则n的值为14. 若关于x的方程x2-mx+m=0有两个相等实根,则代数式2m2-8m+1的值为 .15. 已知a,b,c是△ABC的三边长,若方程(a-c)x2+2bx+a+c=0有两个相等的实数根,则△ABC是 三角形.16. 从3,0,﹣1,﹣2,﹣3这五个数中抽取一个数,作为函数y=(5﹣m2)x和关于x的一元二次方程(m+1)x2+mx+1=0中m的值.若恰好使函数的图象经过第一、三象限,且使方程有实数根,则满足条件的m的值是 .
三、解答题
-
17. 已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)、证明:不论m为何值时,方程总有实数根;(2)、m为何整数时,方程有两个不相等的正整数根.18. 已知:关于x的方程x2+2mx+m2-1=0(1)、不解方程,判别方程根的情况;(2)、若方程有一个根为3,求m的值.19. 已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.(1)、若该方程有两个实数根,求m的最小整数值;(2)、若方程的两个实数根为x1 , x2 , 且(x1﹣x2)2+m2=21,求m的值.