2018-2019学年数学北师大版八年级上册第三章《位置与坐标》单元测试卷
试卷更新日期：2018-09-03 类型：单元试卷
一、选择题：
-
1. 已知直角坐标系内有一点M（a，b），且ab=0，则点M的位置一定在（ ）
A、原点上 B、x轴上 C、y轴上 D、坐标轴上2. 已知点A（a，3）和点B（4，b）关于y轴对称，则a+b的值是（ ）
A、1 B、－1 C、7 D、－73. 已知点P关于x轴的对称点为（a，-2），关于y轴对称点为（1，b），那么点P的坐标为（ ）
A、（a， －b） B、(b， －a) C、(－2，1) D、(－1，2)4. 点P（m＋3， m＋1）在直角坐标系的x轴上，则点P坐标为（ ）A、（0，－2） B、（ 2，0） C、（4，0） D、（0，－4）5. 如图，若将△ABC绕点O逆时针旋转90°，则顶点B的对应点B1的坐标为（ ）
A、（－4，2） B、（－2，4） C、（4，－2） D、（2，－4）6. 已知点P（a，b），ab＞0，a＋b ＜0，则点P在（ ）象限
A、一 B、二 C、三 D、四7. 一个长方形在平面直角坐标系中三个顶点的坐标为（– 1，– 1）.（– 1，2）.（3，– 1），则第四个顶点的坐标为（ ）
A、（2，2） B、（3，2） C、（3，3） D、（2，3）8. 在平面直角坐标系中，点A的坐标为（－1， ），以原点O为中心，将点A顺时针旋转150°得到点A′，则点A′的坐标为（ ）
A、（0，－2） B、（1，－ ） C、（2，0） D、（ ，－1）9. 如图，在平面直角坐标系中，点A，B的坐标分别是A（3，0），B（0，4），把线段AB绕点A旋转后得到线段AB′，使点B的对应点B′落在x轴的正半轴上，则点B′的坐标是（ ）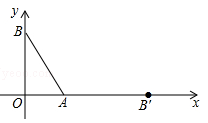
A、（5，0） B、（8，0） C、（0，5） D、（0，8）10. 已知点P（x， |x|），则点P一定（ ）
A、在第一象限 B、在第一或第四象限 C、在x轴上方 D、不在x轴下方11. 在平面直角坐标系中，△ABC位于第二象限，点A的坐标是（－2，3），先把△ABC向右平移4个单位长度得到△A1B1C1 ， 再作与△A1B1C1关于x轴对称的△A2B2C2 ， 则点A的对应点A2的坐标是（ ）A、（－3，2） B、（2，－3） C、（1，－2） D、（－1，2）12. 如图，一个点在第一象限及x轴.y轴上运动，且每秒移动一个单位，在第1秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，那么第35秒时质点所在位置的坐标是（ ）
A、（4，0） B、（0，5） C、（5，0） D、（5，5）二、填空题
-
13. 点（﹣2，﹣3）关于直线x=﹣1的对称点的坐标为 ．
14. 已知点A（a，5）与点A′（﹣2，b）关于经过点（3，0）且平行于y轴的直线对称，那么a+b= ．
15. 如果用（7，8）表示七年级八班，那么八年级七班可表示成.16. 如图，A点的坐标为（－1，5），B点的坐标为（3，3），C点的坐标为（5，3），D点的坐标为（3，－1），小明发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，你认为这个旋转中心的坐标是 ．
三、解答题
-
17. 已知点P（a ， b）在第二象限，且|a|=3，|b|=8，求点P的坐标
18. 如图，A.B两点的坐标分别是（2，﹣3）.（﹣4，﹣3）．
(1)、请你确定P（4，3）的位置；
(2)、请你写出点Q的坐标．19. 如图，建立适当的直角坐标系，并写出这个四角星的八个顶点的坐标。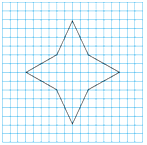
20. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a.b满足 ＋|b－6|＝0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O－C－B－A－O的线路移动．
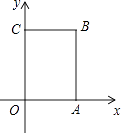(1)、a＝ ， b＝ ， 点B的坐标为；(2)、当点P移动4秒时，请指出点P的位置，并求出点P的坐标；
(3)、在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．21. 在平面直角坐标系中，O为原点，B（0，6），A（8，0），以点B为旋转中心把△ABO逆时针旋转，得△A′BO′，点O，A旋转后的对应点为O′，A′，记旋转角为β．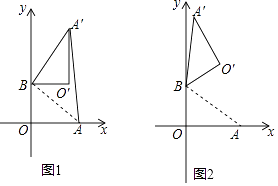
(1)、如图1，若β＝90°，求AA′的长；(2)、如图2，若β＝120°，求点O′的坐标．22. 多多和爸爸、妈妈周末到动物园游玩，回到家后，她利用平面直角坐标系画出了动物园的景区地图，如图所示．可是她忘记了在图中标出原点和x轴、y轴．只知道马场的坐标为（﹣3，﹣3），你能帮她建立平面直角坐标系并求出其他各景点的坐标？
23. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S＝ah．例如：三点坐标分别为A（1，2），B（－3，1），C（2，－2），则“水平底”a＝5，“铅垂高”h＝4，“矩面积”S＝ah＝20．根据所给定义解决下列问题：
(1)、若已知点D（1，2）.E（－2，1）.F（0，6），则这3点的“矩面积”＝ ．
(2)、若D（1，2）.E（－2，1）.F（0，t）三点的“矩面积”为18，求点F的坐标．