2018-2019学年数学湘教版九年级上册第一章反比例函数单元检测b卷

试卷更新日期：2018-08-29 类型：单元试卷

进入出卷网下载

一、选择题

1. 设A( $x_{1}$ ， $y_{1}$ )，B ( $x_{2}$ ， $y_{2}$ )是反比例函数 $y = - \frac{2}{x}$ 图像上的两点，若 $x_{1}$ < $x_{2}$ <0则 $y_{1}$ 与 $y_{2}$ 之间的关系是（）

A、 $y_{1}$ < $y_{2}$ <0 B、 $y_{2}$ < $y_{1}$ <0 C、 $y_{2}$ > $y_{1}$ >0 D、 $y_{1}$ > $y_{2}$ >0

查看试题解析
2. 已知反比例函数 $y = \frac{2}{x}$ ，下列结论中，不正确的是（）

A、图象必经过点（1，2） B、y随x的增大而减少 C、图象在第一、三象限内 D、若x＞1，则y＜2

查看试题解析
3. 一次函数y=ax+b与反比例函数y＝ $\frac{c}{x}$ 的图象如图所示，则（）

A、a＞0，b＞0．c＞0 B、a＜0，b＜0．c＜0 C、a＜0，b＞0．c＞0 D、a＜0，b＜0．c＞0

查看试题解析
4. 若反比例函数y＝ $\frac{2 a - 3}{x}$ 的图象位于第一、三象限，则a的取值范围是（）

A、a＞0 B、a＞3 C、a＞ $\frac{3}{2}$ D、a＜ $\frac{3}{2}$

查看试题解析
5. 如图，已知双曲线y＝ $\frac{k}{x}$ （k>0）经过Rt△OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为6，则k的值为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 将点P（4，3）向下平移1个单位后，落在反比例函数y＝ $\frac{k}{x}$ 的图象上，则k的值为（）

A、12 B、10 C、9 D、8

查看试题解析
7. 已知点P（1，﹣3）在反比例函数y= $\frac{k}{x}$ （k≠0）的图象上，则k的值是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
8. 已知函数y=（m﹣2） $x^{m^{2} - 5}$ 是反比例函数，则m的值为（）

A、2 B、﹣2 C、2或﹣2 D、任意实数

查看试题解析
9. 如图，点A在反比例函数 $y = \frac{3}{x} (x > 0)$ 的图象上，点B在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上，AB⊥x轴于点M，且AM：MB=1：2，则k的值为（）

A、3 B、－6 C、2 D、6

查看试题解析
10. 如图，反比例函数 $y = \frac{k}{x}$ （k＞0）与一次函数 $y = \frac{1}{2} x + 4$ 的图象相交于两点A( $x_{1}$ ， $y_{1}$ )，B( $x_{2}$ ， $y_{2}$ )，线段AB交y轴与C，当| $x_{1}$ － $x_{2}$ |=2且AC = 2BC时，k、b的值分别为（）

A、k＝ $\frac{1}{2}$ ，b＝2 B、k＝ $\frac{4}{9}$ ，b＝1 C、k＝ $\frac{1}{3}$ ，b＝ $\frac{1}{3}$ D、k＝ $\frac{4}{9}$ ，b＝ $\frac{1}{3}$

查看试题解析

二、填空题

11. 反比例函数 $y = \frac{k}{x}$ 的图象经过点（2，－1），则k的值为.

查看试题解析
12. 如上图，反比例函数 $y = \frac{k}{x}$ 的图象位于第一、三象限，其中第一象限内的图象经过点A（1，2），请在第三象限内的图象上找一个你喜欢的点P，你选择的P点坐标为．

查看试题解析
13. 函数 $y_{1} = x (x \geq 0) ， y_{2} = \frac{4}{x} (x > 0)$ 的图象如图所示，则结论：
①两函数图象的交点 $A$ 的坐标为 $(2 ， 2)$ ； ②当 $x > 2$ 时， $y_{2} > y_{1}$ ；③当 $x = 1$ 时， $B C = 3$ ；④当 $x$ 逐渐增大时， $y_{1}$ 随着 $x$ 的增大而增大， $y_{2}$ 随着 $x$ 的增大而减小．
其中正确结论的序号是．

查看试题解析
14. 如图，正比例函数与反比例函数的图象相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆，若点A的坐标为(1，2)，则图中两个阴影面积的和是．

查看试题解析
15. 如图，△ABC的三个顶点分别为A（1，2），B（2，5），C（6，1）．若函数y= $\frac{k}{x}$ 在第一象限内的图象与△ABC有交点，则k的取值范围是．

查看试题解析
16. 如图，在平面直角坐标系中，经过点A的双曲线 $y = \frac{k}{x} (x > 0)$ 同时经过点B，且点A在点B的左侧，点A的横坐标为 $\sqrt{2}$ ，∠AOB=∠OBA=45°，则 $k$ 的值为.

查看试题解析

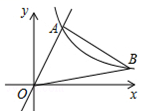
三、解答题

17. 已知y是x的反比例函数，且当x=-4时，y= $\frac{1}{2}$ ，

(1)、求这个反比例函数关系式和自变量x的取值范围；

(2)、求当x=6时函数y的值.

查看试题解析
18. 如图，已知某一次函数与反比例函数的图象相交于A(1，3)，B(m，1)，求：

(1)、m的值与一次函数的解析式；

(2)、△ABO的面积．

查看试题解析
19. 如图，已知直线y= $\frac{3}{2}$ x与反比例函数y= $\frac{k}{x}$ （x＞0）的图象交于点A（2，m）；将直线y= $\frac{3}{2}$ x向下平移后与反比例函数y= $\frac{k}{x}$ （x＞0）的图象交于点B，且△AOB的面积为3．

(1)、求k的值；

(2)、求平移后所得直线的函数表达式．

查看试题解析
20. 如图，在平面直角坐标系中，将坐标原点O沿x轴向左平移2个单位长度得到点A，过点A作y轴的平行线交反比例函数 $y = \frac{k}{x}$ 的图象于点B，AB= $\frac{3}{2}$ ．

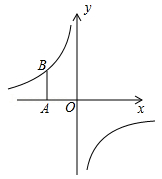(1)、求反比例函数的解析式；

(2)、若P（ $x_{1}$ ， $y_{1}$ ）、Q（ $x_{2}$ ， $y_{2}$ ）是该反比例函数图象上的两点，且 $x_{1} < x_{2}$ 时， $y_{1} > y_{2}$ ，指出点P、Q各位于哪个象限？并简要说明理由．

查看试题解析
21. 如图，直线 $y = x + m$ 与双曲线 $y = \frac{k}{x}$ 相交于A（2，1）、B两点．

(1)、求m及k的值；

(2)、不解关于x、y的方程组 ${\begin{matrix} y = x + m \\ y = \frac{k}{x} \end{matrix}$ 直接写出点B的坐标；

(3)、直线 $y = - 2 x + 4 m$ 经过点B吗？请说明理由．

查看试题解析
22. 某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本Q（元）与月产销量y（个）满足如下关系：
月产销量y（个）
…
160
200
240
300
…
每个玩具的固定成本Q（元）
…
60
48
40
32
…

(1)、写出月产销量y（个）与销售单价x （元）之间的函数关系式；

(2)、求每个玩具的固定成本Q（元）与月产销量y（个）之间的函数关系式；

(3)、若每个玩具的固定成本为30元，则它占销售单价的几分之几？

(4)、若该厂这种玩具的月产销量不超过400个，则每个玩具的固定成本至少为多少元？销售单价最低为多少元？

查看试题解析
23. 如图，在平面直角坐标系中，一次函数y=k₁x+b的图象与反比例函数y= $\frac{k_{2}}{x}$ 的图象交于A（4，﹣2）、B（﹣2，n）两点，与x轴交于点C．

(1)、求k₂ ， n的值；

(2)、请直接写出不等式k₁x+b< $\frac{k_{2}}{x}$ 的解集；

(3)、将x轴下方的图象沿x轴翻折，点A落在点A′处，连接A′B，A′C，求△A′BC的面积．

查看试题解析
24. 某气球内充满了一定质量的气球，当温度不变时，气球内气球的压力p(千帕)是气球的体积V(米²)的反比例函数，其图象如图所示(千帕是一种压强单位)

(1)、写出这个函数的解析式；

(2)、当气球的体积为0.8立方米时，气球内的气压是多少千帕；

(3)、当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米。

查看试题解析
25. 如图，反比例函数 $y_{1} = \frac{m}{x}$ 的图像与一次函数 $y_{2} = k x + b$ 的图像交于A、B两点．已知A (2，n），B（ $- \frac{1}{2} ， - 2$ ）．

(1)、求反比例函数和一次函数的解析式；

(2)、求△AOB的面积；

(3)、请结合图像直接写出当y₁≥y₂时自变量x的取值范围．

查看试题解析

月产销量y（个）	…	160	200	240	300	…
每个玩具的固定成本Q（元）	…	60	48	40	32	…

2018-2019学年数学湘教版九年级上册第一章 反比例函数 单元检测b卷

一、选择题

二、填空题

三、解答题

2018-2019学年数学湘教版九年级上册第一章反比例函数单元检测b卷