2018-2019学年数学湘教版九年级上册第一章反比例函数单元检测a卷

试卷更新日期：2018-08-29 类型：单元试卷

进入出卷网下载

一、选择题

1. 已知反比例函数y＝ $\frac{k}{x}$ 的图象经过点(3，2)，那么下列四个点中，也在这个函数图象上的是（）

A、(3，－2) B、(－2，－3) C、(1，－6) D、(－6，1)

查看试题解析
2. 点A（–2，5）在反比例函数y= $\frac{k}{x}$ （k≠0）的图象上，则k的值是（）

A、10 B、5 C、–5 D、–10

查看试题解析
3. 下面的函数是反比例函数的是（）

A、y＝3x－1 B、y＝ $\frac{x}{2}$ C、y＝ $\frac{1}{3 x}$ D、y＝ $\frac{2 x - 1}{3}$

查看试题解析
4. 已知反比例函数y=﹣ $\frac{6}{x}$ ，下列各点中，在其图象上的有（）

A、（﹣2，﹣3） B、（2，3） C、（2，﹣3） D、（1，6）

查看试题解析
5. 下列选项中，能写成反比例函数的是（　　）

A、人的体重和身高 B、正三角形的边长和面积 C、速度一定，路程和时间的关系 D、销售总价不变，销售单价与销售数量的关系

查看试题解析
6. 已知函数y=k₁x和 $y = \frac{k_{2}}{x}$ ，若常数k₁ ， k₂异号，且k₁＞k₂ ，则它们在同一坐标系内的图象大致是（如图所示）（）

A、 B、 C、 D、

查看试题解析
7. 如图，已知点A是双曲线y＝ $\frac{2}{x}$ 在第一象限的分支上的一个动点，连接AO并延长交另一分支于点B，过点A作y轴的垂线，过点B作x轴的垂线，两垂线交于点C，随着点A的运动，点C的位置也随之变化．设点C的坐标为(m，n)，则m，n满足的关系式为（）

A、n＝－2m B、n＝－ $\frac{2}{m}$ C、n＝－4m D、n＝－ $\frac{4}{m}$

查看试题解析
8. 如图，正比例函数y₁与反比例函数y₂相交于点E（﹣1，2），若y₁＞y₂＞0，则x的取值范围在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
9. 已知反比例函数 $y = - \frac{2}{x}$ ，有下列四个结论：① 图象必经过点(－1，2)；② 图像经过（ $x_{1} ， y_{1}$ ），（ $x_{2} ， y_{2}$ ）两点，若 $x_{1} < x_{2}$ ，则 $y_{1} < y_{2}$ ；③ 图象分布在第二、四象限内；④ 若x＞1，则y＞－2．其中正确的有（）

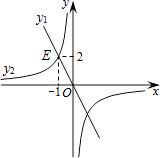A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在平面直角坐标系中，一条直线与反比例函数y= $\frac{8}{x}$ （x＞0）的图象交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数y= $\frac{2}{x}$ （x＞0）的图象交于两点D、E，连接DE，则四边形ABED的面积为（）

A、4 B、 $\frac{9}{2}$ C、5 D、 $\frac{11}{2}$

查看试题解析

二、填空题

11. 在函数 $y = \frac{- k^{2} - 2}{x}$ （ $k$ 为常数）的图象上有三个点 $(- 2 ， y_{1})$ ， $(- 1 ， y_{2})$ ， $(\frac{1}{2} ， y_{3})$ ，将 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 用“ $<$ ”号连接为.

查看试题解析
12. 已知 $y = (m + 3) x^{m^{2} + 5 m + 5}$ ，当 $m$ ＝时， $y$ 是 $x$ 的反比例函数．

查看试题解析
13. 已知反比例函数 $y = \frac{1 - m}{x}$ 的图象在第一、第三象限，则m的取值范围是.

查看试题解析
14. 某厂有煤1500吨，求得这些煤能用的天数y与每天用煤的吨数x之间的函数关系为．

查看试题解析
15. 反比例函数 $y = \frac{3}{x}$ 图象上三个点的坐标为 $(x_{1} ， y_{1})$ 、 $(x_{2} ， y_{2})$ 、 $(x_{3} ， y_{3})$ ，若 $x_{1} < x_{2} < 0 < x_{3}$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是．

查看试题解析
16. 如图，已知点A₁ ， A₂ ， …，A_n均在直线y=x﹣2上，点B₁ ， B₂ ， …，B_n均在双曲线y=﹣ $\frac{4}{x}$ 上，并且满足：A₁B₁⊥x轴，B₁A₂⊥y轴，A₂B₂⊥x轴，B₂A₃⊥y轴，…，A_nB_n⊥x轴，B_nA_n+1⊥y轴，…，记点A_n的横坐标为a_n（n为正整数）．若a₁=﹣2，则a₂₀₁₆= ．

查看试题解析
17. 如图，已知直线 $y = \frac{1}{2} x$ 与反比例函数 $y = \frac{8}{x}$ （ $x > 0$ ）图像交于点A，将直线向右平移4个单位，交反比例函数 $y = \frac{8}{x}$ （ $x > 0$ ）图像于点B，交y轴于点C，连结AB、AC，则△ABC的面积为．

查看试题解析
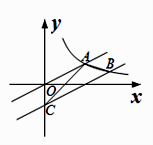18. 如图， $△ O A C$ 和 $△ B A D$ 都是等腰直角三角形， $∠ A C O = ∠ A D B = 90^{\circ}$ ，反比例函数 $y = \frac{k}{x}$ 在第一象限的图象经过点B．

(1)、若 $O C = 3$ ， $B D = 2$ ，则 $k =$ ；

(2)、若 $O A^{2} - A B^{2} = 18.$ 则 $k =$ ．

查看试题解析

三、解答题

19. 已知函数y＝ $\frac{k}{x}$ 的图象经过点(－3，4)．

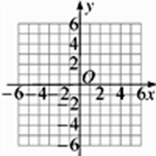(1)、求k的值，并在正方形网格中画出这个函数的图象；

(2)、当x取什么值时，函数的值小于0?

查看试题解析
20. 已知反比例函数y＝ $\frac{m - 5}{x}$ (m为常数，且m≠5)．

(1)、若在其图象的每个分支上，y随x的增大而增大，求m的取值范围；

(2)、若其图象与一次函数y＝－x＋1图象的一个交点的纵坐标是3，求m的值．

查看试题解析
21. 如图，已知一次函数y=k₁x+b的图象与反比例函数y= $\frac{k_{2}}{x}$ 的图象交于A（1，-3），B（3，m）两点，连接OA、OB．

(1)、求两个函数的解析式；

(2)、求△AOB的面积．

查看试题解析
22. 在平面直角坐标系xOy中，直线y=2x+l与双曲线y= $\frac{k}{x}$ 的一个交点为A（m，-3）．

(1)、求双曲线的表达式；

(2)、过动点P（n，0）（n＜0）且垂直于x轴的直线与直线y=2x+l和双曲线y= $\frac{k}{x}$ 的交点分别为B，C，当点B位于点C上方时，直接写出n的取值范围．

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y = a x + b$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于点A（1，3）和B（-3， $m$ ）．

(1)、求一次函数和反比例函数的解析式；

(2)、点C是平面直角坐标系内一点，BC∥ $x$ 轴，AD⊥BC于点D，连结AC，若 $A C = \sqrt{5} C D$ ，求点C的坐标．

查看试题解析
24. 如图，一次函数y₁= $x$ +1的图象与反比例函数 $y_{2} = \frac{k}{x}$ （k为常数，且k≠0）的图象都经过点A（m，2）．

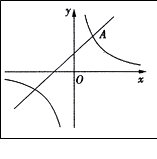(1)、求点A的坐标及反比例函数的表达式；

(2)、结合图象直接比较：当 $x$ ＞0时， $y_{1}$ 与 $y_{2}$ 的大小．

查看试题解析
25. 月电科技有限公司用160万元，作为新产品的研发费用，成功研制出了一种市场急需的电子产品，已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件，在销售过程中发现：每年的年销售量 $y$ (万件)与销售价格 $x$ （元/件）的关系如图所示，其中AB为反比例函数图象的一部分，BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为 $z$ （万元）.（注：若上一年盈利，则盈利不计入下一年的年利润；若上一年亏损，则亏损计作下一年的成本.）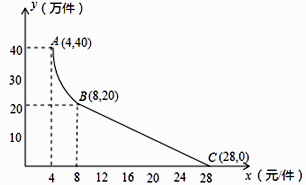

(1)、请求出 $y$ （万件）与 $x$ （元/件）之间的函数关系式；

(2)、求出第一年这种电子产品的年利润 $z$ （万元）与 $x$ （元/件）之间的函数关系式，并求出第一年年利润的最大值；

(3)、假设公司的这种电子产品第一年恰好按年利润 $z$ （万元）取得最大值时进行销售，现根据第一年的盈亏情况，决定第二年将这种电子产品每件的销售价格 $x$ （元）定在8元以上（ $x > 8$ ），当第二年的年利润不低于103万元时，请结合年利润 $z$ （万元）与销售价格 $x$ （元/件）的函数示意图，求销售价格 $x$ （元/件）的取值范围.

查看试题解析

2018-2019学年数学湘教版九年级上册第一章 反比例函数 单元检测a卷

一、选择题

二、填空题

三、解答题

2018-2019学年数学湘教版九年级上册第一章反比例函数单元检测a卷