2018-2019学年数学湘教版九年级上册1.3 反比例函数的应用 同步练习
试卷更新日期:2018-08-29 类型:同步测试
一、选择题
-
1. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积 x(mL) 100 80 60 40 20 压强 y(kPa) 60 75 100 150 300
A、 000x B、 000x C、 D、2. 已知用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,则下列说法中,正确的是( )
A、当P为定值时,I与R成反比例; B、当P为定值时,I2与R成反比例 C、当P为定值时,I与R成正比例; D、当P为定值时,I2与R成正比例3. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 p(kPa)是气体体积 V(m 3)的反比例函数,其图象如图所示.当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应( )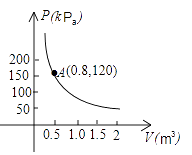 A、不大于 m3 B、不小于 m3 C、不大于 m 3 D、不小于 m 34. 某乡粮食总产量为a(常数)吨,设该乡平均每人占有粮食为y吨,人口数为x,则y与x之间的函数关系的图象是( )
A、不大于 m3 B、不小于 m3 C、不大于 m 3 D、不小于 m 34. 某乡粮食总产量为a(常数)吨,设该乡平均每人占有粮食为y吨,人口数为x,则y与x之间的函数关系的图象是( )
A、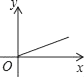 B、
B、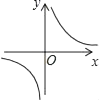 C、
C、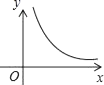 D、
D、 5. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
5. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( ) A、当x=3时,EC<EM B、当x=9时,EC<EM C、当x增大时,BE·DF的值不变 D、当x增大时,EC·CF的值增大6. 如图,过点O作直线与双曲线 (k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1 , △EOF的面积为S2 , 则S1、S2的数量关系是( ).
A、当x=3时,EC<EM B、当x=9时,EC<EM C、当x增大时,BE·DF的值不变 D、当x增大时,EC·CF的值增大6. 如图,过点O作直线与双曲线 (k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1 , △EOF的面积为S2 , 则S1、S2的数量关系是( ). A、S1=S2 B、2S1=S2 C、3S1=S2 D、4S1=S27. 若 ,则在同一直角坐标系中,直线y= x-a与双曲线y= 的交点个数为( )
A、S1=S2 B、2S1=S2 C、3S1=S2 D、4S1=S27. 若 ,则在同一直角坐标系中,直线y= x-a与双曲线y= 的交点个数为( )
A、0 B、1 C、2 D、38. 某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为. 9. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
9. 某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) A、该村人均耕地面积随总人口的增多而增多 B、该村人均耕地面积y与总人口x成正比例 C、若该村人均耕地面积为2公顷,则总人口有100人 D、当该村总人口为50人时,人均耕地面积为1公顷10. 如图,平面直角坐标系中,矩形OABC的顶点B在第一象限,点C在x轴上,点A在y轴上,D、E分别是AB,OA中点.过点D的双曲线 与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ).
A、该村人均耕地面积随总人口的增多而增多 B、该村人均耕地面积y与总人口x成正比例 C、若该村人均耕地面积为2公顷,则总人口有100人 D、当该村总人口为50人时,人均耕地面积为1公顷10. 如图,平面直角坐标系中,矩形OABC的顶点B在第一象限,点C在x轴上,点A在y轴上,D、E分别是AB,OA中点.过点D的双曲线 与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ). A、 B、 C、6 D、10
A、 B、 C、6 D、10二、填空题
-
11. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(kg/m3)是体积V(m3)的反比例函数,它的图象如图所示.当V=5m3时,气体的密度是kg/m3 .
 12. 近视眼镜的度数y度与镜片焦距x米呈反比例,其函数关系式为 如果近似眼镜镜片的焦距 米,那么近视眼镜的度数y为 .
12. 近视眼镜的度数y度与镜片焦距x米呈反比例,其函数关系式为 如果近似眼镜镜片的焦距 米,那么近视眼镜的度数y为 .
13. 如图,A,B是双曲线 上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若OD=2BD,△ADO的面积为1,则k的值为 . 14. 如图所示蓄电池的电压为定值,使用该蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的电器的限制电流不超过12A,那么用电器可变电阻R应控制的范围是 .
14. 如图所示蓄电池的电压为定值,使用该蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的电器的限制电流不超过12A,那么用电器可变电阻R应控制的范围是 . 15. 如图,点A是反比例函数 在第二象限内图像上一点,点B是反比例函数 在第一象限内图像上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则 的面积是。
15. 如图,点A是反比例函数 在第二象限内图像上一点,点B是反比例函数 在第一象限内图像上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,则 的面积是。 16. 某中学要在校园内划出一块面积为100m2的三角形土地做花圃,设这个三角形的一边长为xm,这条边上的高为ym,那么y关于x的函数解析式是 , 它是一个函数.
16. 某中学要在校园内划出一块面积为100m2的三角形土地做花圃,设这个三角形的一边长为xm,这条边上的高为ym,那么y关于x的函数解析式是 , 它是一个函数.
三、解答题
-
17. 一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
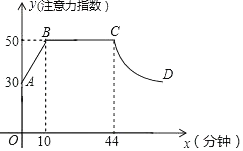 (1)、分别求出线段AB和双曲线CD的函数关系式;
(1)、分别求出线段AB和双曲线CD的函数关系式;
(2)、若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?
18. 如图为某种材料温度y(℃)随时间x(min)变化的函数图象.已知该材料初始温度为15 ℃,
温度上升阶段y与时间x成一次函数关系,且在第5分钟温度达到最大值60 ℃后开始下降;温度下降阶段,温度y与时间x成反比例关系. (1)、分别求该材料温度上升和下降阶段,y与x间的函数关系式;
(1)、分别求该材料温度上升和下降阶段,y与x间的函数关系式;
(2)、根据工艺要求,当材料的温度高于30 ℃时,可以进行产品加工,问可加工多长时间?
19. 码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图. (1)、求y与x之间的函数表达式;
(1)、求y与x之间的函数表达式;
(2)、由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)、若原有码头工人10名,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
20. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 的一部分.请根据图中信息解答下列问题: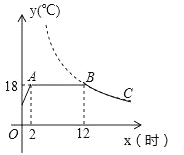 (1)、恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(1)、恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)、求k的值;(3)、当x=15时,大棚内的温度约为多少度?21. 某农户共摘收水蜜桃1920千克,为寻求合适的销售价格,进行了6天试销,试销情况如下:第1天
第2天
第3天
第4天
第5天
第6天
售价
x(元/千克)
20
18
15
12
10
9
销售量
y(千克)
45
50
60
75
90
100
由表中数据可知,试销期间这批水蜜桃的每天销售量y(千克)与售价x(元/千克)之间满足我们曾经学过的某种函数关系.若在这批水蜜桃的后续销售中,每天的销售量y(千克)与售价x(元/千克)之间都满足这一函数关系.
(1)、你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.(2)、在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.① 若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
② 该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?
22. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题: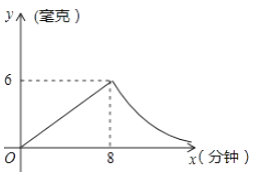 (1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
(1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?