2018-2019学年数学沪科版九年级上册21.2 二次函数的图象和性质（1）同步练习

试卷更新日期：2018-08-28 类型：同步测试

进入出卷网下载

一、选择题

1. 已知点（－1，2）在二次函数y=ax²的图象上，那么a的值是（）

A、1 B、2 C、 $\frac{1}{2}$ D、－ $\frac{1}{2}$

查看试题解析
2. 函数y=ax²(a≠0)的图象经过点(a，8)，则a的值为（）

A、±2 B、－2 C、2 D、3

查看试题解析
3. 抛物线y= $\frac{1}{4}$ x² ， y=4x² ， y=－2x²的图像中，开口最大的是（）

A、y= $\frac{1}{4}$ x² B、y=4x² C、y=－2x² D、无法确定

查看试题解析
4. 如图，四个二次函数的图象中，分别对应的是：① 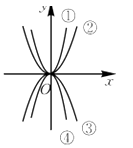$y = a x^{2}$ ；② $y = b x^{2}$ ；③ $y = c x^{2}$ ；④ $y = d x^{2}$ ，则 $a ， b ， c ， d$ 的大小关系为（）

A、 $a > b > c > d$ B、 $a > b > d > c$ C、 D、 $b > a > c > d$

查看试题解析
5. 抛物线y=3x²的顶点坐标是（）

A、（3，0） B、（0，3） C、（0，0） D、（1，3）

查看试题解析
6. 若抛物线 $y = a x^{2}$ 经过点P（1，－3），则此抛物线也经过点（）

A、P $(- 1 ， 3)$ B、P $(- 3 ， 1)$ C、P (1，3) D、P $(- 1 ， - 3)$

查看试题解析
7. 在同一坐标系中，抛物线 $y = 2 x^{2}$ ， $y = \frac{1}{2} x^{2}$ ， $y = - \frac{1}{2} x^{2}$ 的共同特点是（）

A、关于y轴对称，开口向上 B、关于y轴对称，y随x增大而减小 C、关于y轴对称，y随x增大而增大 D、关于y轴对称，顶点在原点

查看试题解析
8. 已知点（-2， $y_{1}$ ），（0， $y_{2}$ ），（1， $y_{3}$ ）都在函数 $y = x^{2}$ 的图象上，则（）

A、 $y_{2}$ ＞ $y_{3}$ ＞ $y_{1}$ B、 $y_{1}$ ＞ $y_{3}$ ＞ $y_{2}$ C、 $y_{3}$ ＞ $y_{2}$ ＞ $y_{1}$ D、 $y_{2}$ ＞ $y_{1}$ ＞ $y_{3}$

查看试题解析
9. 已知a<－1，点（a－1，y₁），（a，y₂），（a+1，y₃）都在函数y=x²的图象上，则（）

A、y₁<y₂<y₃ B、y₁<y₃<y₂ C、y₃<y₂<y₁ D、y₂<y₁<y₃

查看试题解析
10. 下列说法中错误的是（）

A、在函数 $y = - x^{2}$ 中，当 $x = 0$ 时 $y$ 有最大值 $0$ B、在函数 $y = 2 x^{2}$ 中，当 $x > 0$ 时 $y$ 随 $x$ 的增大而增大 C、抛物线 $y = 2 x^{2}$ ， $y = - x^{2}$ ， $y = - \frac{1}{2} x^{2}$ 中，抛物线 $y = 2 x^{2}$ 的开口最小，抛物线 $y = - x^{2}$ 的开口最大 D、不论 $a$ 是正数还是负数，抛物线 $y = a x^{2}$ 的顶点都是坐标原点

查看试题解析
11. 如图，在平面直角坐标系中，A（1，2），B（1，－1），C（2，2），抛物线y=ax²（a≠0）经过△ABC区域（包括边界），则a的取值范围是（）

A、a≤－1或a≥2 B、 $\frac{1}{2}$ ≤a≤2 C、－1≤a＜0或1＜a≤ $\frac{1}{2}$ D、－1≤a＜0或0＜a≤2

查看试题解析

二、填空题

12. 已知二次函数 $y = (m - 2) x^{2}$ 的图象开口向下，则m的取值范围是．

查看试题解析
13. 写出一个开口向上，顶点是坐标原点的二次函数的解析式：.

查看试题解析
14. 某抛物线有以下性质：①开口向下；②对称轴是y轴；③与x轴不相交；④最高点是原点．其中y=﹣2x²具有的性质是．（填序号）

查看试题解析
15. 抛物线y＝2x²的顶点，坐标为，对称轴是．当x时，y随x增大而减小；当x时，y随x增大而增大；当x＝时，y有最值是．

查看试题解析
16. 如图，正方形的边长为4，以正方形中心为原点建立平面直角坐标系，作出函数y= $\frac{1}{3}$ x²与y=– $\frac{1}{3}$ x²的图象，则阴影部分的面积是．

查看试题解析
17. 若抛物线y=ax²经过点A ( $\sqrt{3}$ ，－9)，则其解析式为。

查看试题解析
18. 已知二次函数y_甲=mx²和y_乙=nx² ，对任意给定一个x值都有y_甲≥y_乙，关于m，n的关系正确的是(填序号).①m<n<0 ②m>0，n<0 ③m<0，n>0 ④m>n>0

查看试题解析
19. 如图，已知A₁ ， A₂ ， A₃ ， …，A_n是x轴上的点，且OA₁＝A₁A₂＝A₂A₃＝…＝A_n_－₁A_n＝1，分别过点A₁ ， A₂ ， A₃ ， …，A_n作x轴的垂线交二次函数y＝ $\frac{1}{2}$ x²(x＞0)的图象于点P₁ ， P₂ ， P₃ ， …，P_n ，若记△OA₁P₁的面积为S₁ ，过点P₁作P₁B₁⊥A₂P₂于点B₁ ，记△P₁B₁P₂的面积为S₂ ，过点P₂作P₂B₂⊥A₃P₃于点B₂ ，记△P₂B₂P₃的面积为S₃……依次进行下去，则S₃＝，最后记△P_n_－₁B_n_－₁P_n(n＞1)的面积为S_n ，则S_n＝．

查看试题解析

三、解答题

20. 已知 $y = (k + 2) x^{k^{2} + k - 4}$ 是二次函数，且函数图象有最高点．

(1)、求k的值；

(2)、求顶点坐标和对称轴，并说明当x为何值时，y随x的增大而减少．

查看试题解析
21. 已知点A（2，a）在抛物线y=x²上

(1)、求A点的坐标；

(2)、在x轴上是否存在点P，使△OAP是等腰三角形？若存在写出P点坐标；若不存在，说明理由．

查看试题解析
22. 函数y=ax²（a≠0）与直线y=2x-3的图象交于点（1，b）．
求：

(1)、a和b的值；

(2)、求抛物线y=ax²的开口方向、对称轴、顶点坐标；

(3)、作y=ax²的草图．

查看试题解析
23. 在同一个直角坐标系中作出y＝ $\frac{1}{2}$ x² ， y＝ $\frac{1}{2}$ x²－1的图象．

(1)、分别指出它们的开口方向、对称轴以及顶点坐标；

(2)、抛物线y＝ $\frac{1}{2}$ x²－1与抛物线y＝ $\frac{1}{2}$ x²有什么关系？

查看试题解析
24. 已知抛物线y＝ax²经过点(1，3)．

(1)、求a的值；

(2)、当x＝3时，求y的值；

(3)、说出此二次函数的三条性质．

查看试题解析
25. 如图，直线AB过x轴上一点A（2，0），且与抛物线y=ax²相交于B、C两点，B点坐标为（1，1）．

(1)、求直线AB的解析式及抛物线y=ax²的解析式；

(2)、求点C的坐标；

(3)、求S_△_COB ．

查看试题解析

2018-2019学年数学沪科版九年级上册21.2 二次函数的图象和性质（1） 同步练习

一、选择题

二、填空题

三、解答题

2018-2019学年数学沪科版九年级上册21.2 二次函数的图象和性质（1）同步练习