广东省惠州市2018届数学中考一模试卷

试卷更新日期：2018-08-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果零上2℃记作+2℃，那么零下3℃记作（）

A、+2℃ B、﹣2℃ C、+3℃ D、﹣3℃

查看试题解析
2. 随着空气质量的恶化，雾霾天气现象增多，危害加重．森林是“地球之肺”，每年能为人类提供大约28.3亿吨的有机物，2830000000可用科学记数法表示为（）

A、28.3×10⁸ B、2.83×10⁹ C、2.83×10 D、2.83×10⁷

查看试题解析
3. 如图，∠1=75°，要使a∥b，则∠2等于（）

A、75° B、95° C、105° D、115°

查看试题解析
4. 方程 $x (x + 2) = 0$ 的根是（）

A、x=2 B、x=0 C、x₁=0，x₂=-2 D、 x₁=0，x₂=2

查看试题解析
5. 数据2，7，3，7，5，3，7的众数是（）

A、2 B、3 C、5 D、7

查看试题解析
6. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
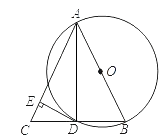
7. 如图，点A的坐标为（1，0），点B在直线y=﹣x上运动，当线段AB最短时，点B的坐标为（）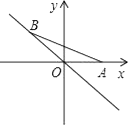

A、（0，0） B、（ $\frac{1}{2}$ ，﹣ $\frac{1}{2}$ ） C、（ $\frac{\sqrt{2}}{2}$ ，﹣ $\frac{\sqrt{2}}{2}$ ） D、（﹣ $\frac{1}{2}$ ， $\frac{1}{2}$ ）

查看试题解析
8. 下列运算中，正确的是（）

A、x³+x³=x⁶ B、x³·x⁹=x²⁷ C、(x²)³=x⁵ D、x $\div$ x²=x^－1

查看试题解析
9. 已知在⊙O 上依次有A、B、C三点，∠AOB=100°，则∠ACB的度数是（）

A、50° B、130° C、50°或l30° D、100°

查看试题解析
10. 已知：如图，在▱ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF于C、H．请判断下列结论：（1）BE=DF；（2）AG=GH=HC；（3）EG= $\frac{1}{2}$ BG；（4）S_△_ABE=3S_△_AGE ．其中正确的结论有（）

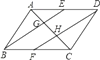A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解：a²﹣6a+9= ．

查看试题解析
12. 已知菱形的两条对角线长分别是6和8，则这个菱形的面积为．

查看试题解析
13. 如果|x|=6，则x= ．

查看试题解析
14. 在一次抽奖活动中，中奖概率是0.12，则不中奖的概率是．

查看试题解析
15. 若3a²﹣a﹣3=0，则5+2a﹣6a²= ．

查看试题解析
16. 如图，在菱形ABCD中，∠B=60°，点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动．给出以下四个结论：
①AE=AF；②∠CEF=∠CFE；③当点E，F分别为边BC，DC的中点时，△AEF是等边三角形；④当点E，F分别为边BC，DC的中点时，△AEF的面积最大．上述结论中正确的序号有．（把你认为正确的序号都填上）

查看试题解析

三、解答题

17. $\sqrt{12}$ +|﹣ $\sqrt{3}$ |﹣（﹣2006）⁰+（ $\frac{1}{2}$ ）^﹣¹

查看试题解析
18. 先化简，再求值：（ $\frac{1}{a - 2}$ + $\frac{1}{a + 2}$ ） $\div \frac{2 a}{a^{2} - 4 a + 4}$ ，其中a=﹣4．

查看试题解析
19. 列方程或方程组解应用题：
“地球一小时”是世界自然基金会在2007年提出的一项倡议．号召个人、社区、企业和政府在每年3月最后一个星期六20时30分﹣21时30分熄灯一小时，旨在通过一个人人可为的活动，让全球民众共同携手关注气候变化，倡导低碳生活．中国内地去年和今年共有119个城市参加了此项活动，且今年参加活动的城市个数比去年的3倍少13个，问中国内地去年、今年分别有多少个城市参加了此项活动．

查看试题解析
20. 如图，在△ABC中，∠B=40°，∠C=80°，按要求完成下列各题：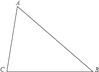

(1)、作△ABC的角平分线AE；

(2)、根据你所画的图形求∠BAE的度数．

查看试题解析
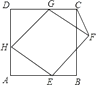
21. 如图，在梯形ABCD中，AD∥BC，AB=DC．点E、F、G分别在边AB、BC、CD上，AE=GF=GC．

(1)、求证：四边形AEFG是平行四边形；

(2)、当∠FGC=2∠EFB时，求证：四边形AEFG是矩形．

查看试题解析
22. 一个不透明的口袋里装有红、黄、绿三种颜色的球（除颜色不同外其余都相同），其中红球有2个，黄球有1个，从中任意捧出1球是红球的概率为 $\frac{1}{2}$ ．

(1)、试求袋中绿球的个数；

(2)、第1次从袋中任意摸出1球（不放回），第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率．

查看试题解析
23. 已知抛物线y=ax²经过点A（﹣2，﹣8）．

(1)、求此抛物线的函数解析式；

(2)、写出这个二次函数图象的顶点坐标、对称轴；

(3)、判断点B（﹣1，﹣4）是否在此抛物线上；

(4)、求出此抛物线上纵坐标为﹣6的点的坐标．

查看试题解析
24. 如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC，过点D作DE⊥AC，垂足为E．

(1)、求证：AB=AC；

(2)、求证：DE为⊙O的切线；

(3)、若⊙O半径为5，∠BAC=60°，求DE的长．

查看试题解析
25. 已知，如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD边AB，CD，DA上，AH=2，连接CF．

(1)、当DG=2时，求△FCG的面积；

(2)、设DG=x，用含x的代数式表示△FCG的面积；

(3)、判断△FCG的面积能否等于1，并说明理由．

查看试题解析